XYLENE POWER LTD.

THEORETICAL SPHEROMAK

By Charles Rhodes, P.Eng., Ph.D.

SPHEROMAK DESCRIPTION:
It is implicity assumed herein that spheromaks are the result of well known electromagnetic field interactions.

A spheromak is a stationary quasi-toroidal solution to Maxwells electromagnetic equations. A spheromak is a stable energy state. Nature uses spheromaks to form stable charge and field energy concentrations generally known as charged particles with rest mass. This web page makes a few simple assumptions about vector fields and using these assumptions shows the existence of spheromaks and quantitatively derives spheromak properties.

FIELD ENERGY DENSITY INSIDE THE SPHEROMAK WALL:
A spheromak arises from an electric current circulating around a closed spiral filament path that causes an internal toroidal magnetic field with an energy density Ut of the form:
Ut = Uto (Ro / R)^2
for:
Rc < Ro < Rs
where:
Ut = Uto
at
R = Ro
 

FIELD ENERGY DENSITY:
The sum of the external electric field energy density Ue and the external magnetic field energy density Up outside the spheromak wall is the external energy density function:
Up + Ue

This energy density function outside the spheromak wall is similar in form to the energy density function arising from a thin ring of radius Ro containing circulating current (Np I) and net charge Qs.

In the far field:
Ue >> Up
and Ue decreases in proportion to [1 / (R^2 + Z^2)]^2. Outside the spheromak wall for R >> Ro and Z >> Ro the field energy density function must equal the known field energy density at R >> Ro and/or Z >> Ro. The external energy density must also equal the known field energy density along the spheromak axis of symmetry where R = 0 and on the equatorial plane. The external field energy density function must equal the internal field energy density function at the spheromak walls.

This web page is concerned with finding mathematical expressions for the spheromak geometry and spheromak electric and magnetic field energy densities for use by other web pages on this web site. It is assumed herein that a spheromak is cylindrically symmetric with the position of any point on the spheromak being defined by its radius R from the main axis of symmetry and its distance Z above the equatorial plane where Z = 0. Outside the spheromak wall the electromagnetic field energy density is given by:
Up(R, Z) + Ue(R,Z) and inside the spheromak wall the electromagnetic field energy density is given by:
Ut(R, Z) = Uto (Ro / R)^2.

The position of the spheromak wall is defined by the locus of points where:
Up(R, Z) + Ue(R, Z) = Ut(R, Z).

It is assumed that inside the spheromak wall there is no net poloidal magnetic field and there is no net electric field.

It is further assumed that outside the spheromak wall there is no net toroidal magnetic field.

The general approach is to find the axial electric and magnetic fields associated with a thin circular closed current ring of radius Ro located at R = Ro, Z = 0 containing uniformly distributed net charge Qs and having Np poloidal turns carrying current I, and then to generalize those expressions to describe a spheromak.

The modified expressions are then used to find the spheromak geometry in terms of well known physical parameters.

Important spheromak parameters are (Rc / Ro), (Rs / Ro) and [Hm / Ro] which indicate the exact shape of the spheromak. These parameters affects the calculated values of the Planck Constant and the Fine Structure Constant.

It is assumed that inside the spheromak wall the only non-zero net field is the toroidal magnetic field given by:
Bt = Muo Nt I / 2 Pi R
so that inside the spheromak wall the toroidal magnetic field energy density is:
Ut = Bt^2 / 2 Muo
= (Muo / 8) [Nt I / Pi R]^2

Inside the spheromak wall all the other field energy density contributions are assumed to be zero.
 

STRATEGY:
This problem is attacked by first finding the field energy densities along the Z axis, then finding the field energy densities on the equatorial plane and then finally by finding the field energy densities elsewhere outside the spheromak wall.

The expressions calculated on this web page are used first to determine Rc and Rs on the equatorial plane and then on the web page titled: SPHEROMAK ENERGY to find the total field energy content of a spheromak. That expression for total field enegy is then used on the web age titled: PLANCK CONSTANT to find both the Planck Constant and the Fine Structure Constant in terms of other physical parameters.

This work provides the fundamental connection between units of energy and units of time which currently are connected only by experimental measurements of the Planck Constant.
 

SPHEROMAK MODEL:
An spheromak wall consists of a single layer winding forming a closed current path which has Np poloidal turns and Nt quasi-toroidal turns. The dimensions, winding spacing and distributed charge are such that there is no net force on the winding anywhere along the current filament path.

Inside the spheromak wall the magnetic field is assumed to be purely toroidal and given by:
Bt = Muo Nt I / (2 Pi R)
where:
R = radius from main axis of symmetry
Muo = permiability of free space
Nt = number of quasi-toroidal turns;
I = circulating current
Pi = length of the perimeter of a circle / circle radius
= 3.14159265

Outside the spheromak wall the magnetic field is assumed to be purely poloidal and identical to the magnetic field produced by a thin ring of radius Ro, in the Z = 0 plane, centered at the origin and carrying current (Np I). However, due to spacial distribution of the winding turns there is no certainty that the magnetic field at the center of the spheromak is the same as would be the case if the all the poloidal turns were concentrated in this thin ring.

Inside the spheromak wall the net electric field is assumed to be zero. Outside the spheromak wall the electric field is assumed to be identical to the electric field produced by a thin ring of radius Ro, on the Z = 0 plane, centered at the origin with uniformly distributed charge Qs.

At the spheromak wall the field energy density inside the wall equals the field energy density outside the wall. This issue determines the exact position of the spheromak wall.

The spheromak wall intersects the equatorial plane at two different radii, R = Rc and R = Rs. At both R = Rc an R = Rs the field energy density just inside the spheromak wall equals the total field energy density just outside the spheromak wall.

Ideally the spheromak wall should have a slope of zero at:
R = Rx = [(Rs + Rc) / 2].
Ideally the spheromak wall Z value predicted by the field equations should equal:
Ho = (Rs + Rc) / 2^0.5
predicted by the spheromak winding analysis at CHARGE FILAMENT PROPERTIES. Inside the spheromak wall the magnetic field is purely toroidal and the net electric field is zero. Outside the spheromak wall the magnetic field is purely poloidal and the electric field is mainly normal to the spheromak wall suface.

In a plasma spheromak the electrons and ions follow similar but opposite spiral paths within the spheromak wall. The positive ions move opposite to the electrons to approximately balance both charge and momentum within the spheromak wall. Within the spheromak wall there is sufficient separation between the opposite flowing electron and ion streams to prevent the energetic electrons being scattered by collisions with the spheromak ions.

A fundamental difference between a plasma spheromak and a quantum particle spheromak is that in a plasma the electrons and ions are of two types and are subject to inertial forces whereas in a quantum charged particle the circulating charge may be composed of only one charge type and that charge has no inertial mass. High energy plasma spheromaks are also subject to relativistic effects.
 

SPHEROMAK WALL CONCEPT:
Assume that three dimensional space is divided into two regions by a thin flexible and moveable closed sheet known as a "Spheromak Wall". There is a quasi-toroidal shaped internal region "t" that exists within a larger external region where "p" indicates a manetic field and "e" indicates an electric field. Assume that fields "p" nd 'e" extend to infinity in all directions. The corresponding spacial energy density functions Ut, Ue and Up are all different. The coordinates are all cylindrical and are centered at the origin.

At every point on the spheromak wall the sum of the electric and poloidal magnetic field energy densities just outside the spheromak wall equals the toroidal magnetic field energy density just inside the spheromak wall. This general statement resolves into different boundary conditions at different points on the spheromak wall. These boundary conditions establish the spheromak wall inner radius Rc on the spheromak equatorial plane, the spheromak wall outer radius Rs on the spheromak equatorial plane and the spheromak wall maximum height Hm above the equatorial plane at:
R = Rx = [(Rs + Rc) / 2].

At the stable spheromak wall position the total field energy densities on both sides of the spheromak wall are equal so that there is no net force (no change in total field energy with respect to spheromak wall position) acting to move the spheromak wall. At that spheromak wall position the total system field energy Ett is at a relative minimum:
dEtt / dX = 0,
where X is the wall position in space and
d^2(Ett) / dX^2 > 0.

If the spheromak wall moves outward from its nominal position the local energy density just outside the wall becomes higher that the local energy density just inside of the wall, which results in a net force that pushes the wall inward. Similarly, if the energy density just inside the wall is larger than the energy density just outside the wall there is a net force that pushes the spheromak wall outward until at the spheromak wall the two energy densities are in balance.

Hence, the spheromak wall spontaneously positions itself to achieve a total spheromnak energy relative minimum.

The spheromak wall is located on the locus of points where the energy density is the same for both the internal and external energy density functions. At the spheromak wall:
Ut = Up + Ue

Note that Rc < Ro < Rs, where:
Rs = spheromak wall maximum outside radius
and
Rc = spheromak wall minimum inside radius.

Spheromaks tend to form because there is a certain degree of random energy motion. If random energy motion can cause a spheromak configuration with a lower total potential energy and a higher total kinetic energy, then part of that kinetic energy may become a photon that is radiated away. The remaining system is left trapped in a lower potential energy (spheromak) state until this spheromak absorbs energy (a photon) from an external source. As long as the density of random sufficiently energetic photons in the system environment is relatively small, spheromaks act as particles with stable local accumulations of field energy (rest mass). The distinguishing factor of spheromaks is Ro which sets the spheromak mass. However, spheromaks potentially have two other distinguishing factors. One is the direction of the toroidal magnetic field with respect to the poloidal magnetic field. The other is the operative family of Np, Nt points. In one case:
P = (Np + 2 Nt)
where:
P = prime number and
Npo = (2 Nto + 1)
with a reduced set of primes meeting:
P = 4 Nto +1 In the other case:
P = Nt + 2 Np
where:
P = prime number
and
Nto = 2 Npo +1
with a rduced set of primes meeting: P = 4 Npo + 1.

These differences manifest themselves in particle magnetic properties.

The spheromak wall is formed from a long closed filament of circulating current. The form of the equations which describe the spheromak wall set the ratio of (Np / Nt) where:
Np = number of spheromak filament poloidal turns
and
Nt = number of spheromak filament quasi-toroidal turns.
Note that Np and Nt are both large integers. Note also that if the spheromak is slightly disturbed dNp and dNt are both small integers.  

SPHEROMAK STRUCTURE:
1) A spheromak wall is composed of a closed spiral current filament of overall length Lh which contains both poloidal and quasi-toroidal turns;
2) Spheromak's net charge Qs is uniformly distributed along filament length Lh.
3) The filament current I is:
I = Qs C / Lh
4) The filament current causes a toroidal magnetic field inside the spheromak wall and a poloidal magnetic field outside the spheromak wall;
5) There is a net zero electric field inside the spheromask wall and there is a spherically radial electric field for large (R^2 + Z^2) outside the spheromak wall;
6) At the exact center of the spheromak at R = 0, Z = 0 the net electric field is zero;
7) Inside the spheromak wall where the total field energy density equals the toroidal field energy density, U takes the form:
Ut = Uto [Ro / R]^2
8) Outside the spheromak wall the total field energy density takes the form:
U = Up(R, Z) + Ue(R, Z)
9) Everywhere at the spheromak wall:
Up(R, Z) + Ue(R, Z) = Ut(R)
10) An important special case is at R = Rc, Z = 0 where:
Upc + Uec = Utc;
This equation is used to find Rc in terms of Ro;
11) An important special case is at R = Rs, Z = 0 where:
Ups + Ues = Uts;
This equation is used to find Rs interms of Ro.
12) An important special case is at R = Ro, Z = Ho where:
U = Uto = (1 / 2 Muo) [Muo Nt I / (2 Pi Ro)]^2
13) Np and Nt are positive integers with no common integer factor other than one.
 

POSITION IN A SPHEROMAK:
A spheromak wall has cylindrical symmetry about its main axis of symmetry and has mirror symmetry about its equatorial plane. A position in a spheromak can be referenced by:
(R, Z, Phi)
where:
R = radius from the main axis of spheromak cylindrical symmetry;
and
Z = height above (or below) the spheromak equatorial plane;
and
Phi = angle around the main axis of symmetry.
 

SPHEROMAK GEOMETRY:
The geometry of a spheromak in free space can be characterized by the following parameters:
R = radius of a general point from the spheromak's main axis of symmetry;
Z = distance of a general point from the spheromak's equatorial plane;
H = a Z value on the spheromak wall;
Ho = the Z value on the spheromak wall corresponding to R = Ro;
Hm = the largest H value on the spheromak wall corresponding to R = Rx = (Rs + Rc) / 2;
Rc = spheromak's minimum equatorial radius;
Rs = spheromak's maximum equatorial radius;
Ro = spheromak's characteristic radius;
Rx = radius of peak value of H
Rw = a R value on the spheromak wall;

The subscript c refers to spheromak "inner wall" surface at the equatorial plane;
The subscript s refers to the spheromak "outer wall" surface at the equatorial plane;
The subscript "o" refers to a value corresponding to R = Ro.
The subscript "or" refers to a value at the origin.
 

SPHEROMAK CROSS SECTIONAL DIAGRAM:
FIX The following diagram shows the cross sectional shape of a spheromak. On this diagram:
Rc / Ro = 0.5
Ro / Ro = 1.0
Rm / Ro = 1.3 Rs / Ro = 2.0
Hm / Ro = 2.2

Note that a spheromak in free space is quasi-toroidal. A real plasma spheromak may be further shape distorted by proximity of containment vacuum chamber walls.
 

FIELD RELATIONSHIPS:
Upc = Utc
Ups = Uts
Utc = Uto (Ro / Rc)^2
Uts = Uto (Ro / Rs)^2
Bp = poloidal magnetic field outside the spheromak wall;
Bt = toroidal magnetic field inside the spheromak wall;
Bpor = Bp|(R= 0, Z = 0) = Muo Np I / 2 Ro
Btc = Bt|(R = Rc, Z = 0) = Muo Nt I / 2 Pi Rc
Bpor / Btc = (Np / Nt)(Pi Rc / Ro)
Btc = Bto (Ro / Rc)
Bpor / Bto = (Bpor / Btc)(Btc / Bto) = (Np Pi / Nt)
This is a key relationship
Bts = Bto (Ro / Rs)
 

SPHEROMAK FILAMENT PARAMETERS
Define:
I = Qs C / Lh = filament current;
C = speed of light = 2.997X 10^8 m /s
Lh = length of closed filament defining charge motion path;
Nt = Integer number of toroidal filament turns contained in Lh;
Np = Integer number of poloidal filament turns contained in Lh;
Lt = length of one purely toroidal filament turn;
Lp = 2 Pi Ro = length of one poloidal filament turn at R = Ro;
Vi = ion velocity along charge motion path
Ve = electron velocity along charge motion path
Q = proton charge
Qs = net spheromak charge
Rhoh = charge per unit length along the filament
C = speed of light
Phi = angle around the spheromak main axis of symmetry
Theta = angle around the spheromak minor axis of symmetry measured with respect to the equatorial plane.
 

SPHEROMAK GEOMETRY:
The geometry of a spheromak can be further characterized by the following parameters:
Rw = radius of a point on the spheromak wall from the main axis of symmetry;
Zw = distance of a point on the spheromak wall from the spheromak's equatorial plane;
At Rw = Ro, Zw = +/- Ho;
Note that:
Ho = Zw|(R = Ro)
 

SPHEROMAK SYMMETRY:
At any point in space the electromagnetic field energy density U is given by: U = (Epsilono / 2)[Er^2 + Ez^2 + Et^2] + (1 / 2 Muo)[Br^2 + Bz^2 + Bt^2]

The electric field energy densities are continuous functions except at a spheromak wall where there is a step change. The magnetic field energy densities are continuous functions except at a spheromak wall where there is a step change.

The spheromak cylindrical and mirror symmetry give outside the spheromak wall:
Et(R, Z) = Et(R, - Z) = 0
Er(R, Z) = Er(R, - Z)
Ez(R, Z) = - Ez (R, - Z)
Br(R, Z) = - Br(R, - Z)
Bz(R, Z) = Bz(R, - Z)
Bt(R, Z) = Bt(R, - Z) = 0
Er(R, 0) = Function;
Ez(R, 0) = 0
Br(R, 0) = 0
Bz(R, 0) = Function
Bt(R, 0) = Function
Bz(0, 0) = [2 Muo Upor]^0.5
 

Outside the spheromak wall:
Bt = 0
and
Et = 0
which gives:
U = (Epsilono / 2)[Er^2 + Ez^2] + (1 / 2 Muo)[Br^2 + Bz^2]

Inside the spheromak wall:
Br = 0 and Bz = 0 and Er = 0 and Ez = 0 giving:
U = (1 / 2 Muo)[Bt^2]

Note that the total field energy densities decrease with increasing distance from R = 0, Z = 0.
 

SPHEROMAK WALL SUMMARY:
A spheromak has a thin symmetrical quasi-toroid shaped closed wall that divides three dimensional space into an external region that extends to infinity from the finite three dimensional internal region. This closed wall is formed from a long single layer wound filament and is known as the spheromak wall. The quasi-toroid shaped internal region and the external region each has its own field energy density distribution. The vector fields of a spheromak act together to maintain a stable spheromak wall shape. The total field energy densities of the two regions are identical at the spheromak wall. Otherwise the position of the spheromak wall would be unstable.

Assume that the spheromak wall is free to move. It will spontaneously position itself such that at every point on the spheromak wall the net force on the wall is zero. Hence the spheromak wall will position itself so as to make the field energy densities at the wall equal on both sides of the wall. The result is that the poloidal magnetic field and the radial electric field will be excluded from the space inside the spheromak wall and the toroid magnetic field will be excluded from the space outside the spheromak wall. This field separation will occur because the system total field energy will decrease as the electric and poloidal magnetic fields inside the spheromk wall are displaced by the toroidal field. In effect current will move within the spheromak wall to enable this field separation.

As shown at Charge and Current Filament Behaviour for any stable spheromak wall the filament current I is given by: I = Qs C /Lh = Rhoh C

SPHEROMAK POTENTIAL ENERGY WELL:
Outside the spheromak wall the field energy density functions obey:
(Up + Ue) < Ut.

Inside the spheromak wall the field energy density functions obey:
(Up + Ue) > Ut

Hence in an environment where Up extends to infinity, the spheromak causes a potential energy well inside the spheromak wall.
 

SPHEROMAK FILAMENT

From the web page titled: Spheromak Structure the winding length Lh is given by:
[Lh / 2 Pi]^2 = Nt^2 [(Rs - Rc) / 2]^2 + [Np^2 / 2] {Rs^2 + Rc^2}
= Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}
= Nt^2 [(Rs - Rc) / 2]^2 + Np^2 [Ro^2]
where:
Ro^2 = [(Rs^^2 + Rc^2) / 2]

For any spheromak:
F = C / Lh
and
I = Qs C / Lh
or
I^2 = Qs^2 C^2 / Lh^2
= Qs^2 C^2 / {[2 Pi]^2 {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}}

Thus the magnetic field energy density inside the spheromak wall takes the form:
Bt^2 / 2 Muo = [Muo Nt I / 2 Pi R]^2 / 2 Muo
= [Muo / 8] [Nt / Pi R]^2 [I^2]
= [Muo / 8] [Nt / Pi R]^2 Qs^2 C^2 / {[2 Pi]^2 {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}}
= [Muo / 32][Qs^2 C^2 / (Pi)^4] [1 / R^2][Nt^2 / {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}}]
= [Muo / 32][Qs C / Pi^2]^2 [1 / Ro^2][Nt^2 / {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}}][Ro / R]^2
= Uto [Ro / R]^2
which gives:
Uto = [Muo / 32][Qs C / Pi^2]^2 [1 / Ro^2][Nt^2 / {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}}]
= [Muo / 32][Qs C / Pi^2]^2 [1 / Ro^3][Ro Nt^2 /{Nt^2 [(Rs - Rc) / 2]^2 + Np^2 Ro^2}]

The corresponding natural frequency is:
F = C / Lh
= C / [2 Pi {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 [(Rs^2 + Rc^2) / 2]}^0.5]

Hence:
Uto = [Muo / 32][Qs^2 C^2 / (Pi)^4] [1 / Ro^2][Nt^2 / {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}}]
= [Muo Qs^2 C / 16 Pi^3 Ro^3][Ro Nt^2 / {Nt^2 [(Rs - Rc) / 2]^2 + Np^2 {(Rs^2 + Rc^2) / 2}^0.5] [F]

Note that inside the spheromak wall the field energy density is proportional to
(Ro^2 / R^2).
 

At the inside wall where R = Rc:
Utc = (Ro / Rc)^2 Uto

This expression can be compared to (Up + Ue) at the inside wall to enable calculation of (Np^2 / Nt^2).
 

SPHEROMAK MATHEMATICAL AND BOUNDARY CONDITION SUMMARY:
Consider a long thin electrically conductive filament. This filament occurs as a single layer winding on the surface of a symmetric quasi-toroid so as to form Np poloidal turns and Nt toroidal turns without any filament cross-overs. The two ends of the filament are connected together to form a closed path. The minor axis of the toroid is located at:
X^2 + Y^2 = Rx^2 on the (X,Y) plane.

The spheromak winding encloses a quasi-toroidal shaped space and is referred to as the spheromak wall.

Imagine a charged ring with radius Ro with the ring center at (X = 0, Y = 0). The major axis of both this imaginary ring and the quasi-toroid is at X = Y = 0.

Assume that current I flows through the filament. The filament has Np turns around the toroid major axis and has Nt turns around the toroid minor axis. The current circulating around the toroid major axis is (Np I) and the current circulating around the toroid minor axis is (Nt I). The filament has net charge Qs uniformly distributed over the filament length Lh so that the filament charge per unit length is:
Qs / Lh.

Any point in space has a characteristic R value given by:
R^2 = X^2 + Y^2.

There are radial electric and poloidal magnetic fields outside the spheromak wall.

From the perspective of poloidal magnetic field outside the spheromak wall, the magnetic field size and geometry is identical to the field that would be produced by circulating current (Np I) flowing in the imaginary ring at:
R = Ro, Z = 0.

From the perspective of the electric fields measured outside the spheromak wall the electric field size and geometry is identical to the field that would be produced by charge Qs concentrated in the ring at
R = Ro, Z = 0.

The electric field energy density at any point (R, Z) outside the spheromak wall is:
Ue(R, Z)
and the poloidal magnetic field energy density at any point (R, Z) outside the spheromak wall is:
Up(R, Z).

In the quasi-toroid shaped space inside the spheromak wall the toroidal magnetic field is:
Bt = (Muo Nt I) / 2 Pi R

At R= Rc the toroidal magnetic field is:
Btc = (Muo Nt I) / 2 Pi Rc

At R= Ro the toroidal magnetic field is:
Bto = (Muo Nt I) / 2 Pi Ro

At R= Rs the toroidal magnetic field is:
Bts = (Muo Nt I) / 2 Pi Rs

Inside the spheromak wall the toroidal magnetic field energy density is:
Ut = Bt^2 / 2 Muo
= [Muo Nt^2 I^2 / 8 Pi^2][1 / R]^2

At R = Ro:
Ut = Uto = [Muo Nt^2 I^2 / 8 Pi^2][1 / Ro]^2

At R = Rc:
Ut = Utc = [Muo Nt^2 I^2 / 8 Pi^2][1 / Rc]^2

At R = Rs:
Ut = Uts = [Muo Nt^2 I^2 / 8 Pi^2][1 / Rs]^2

Hence:
Utc / Uto = (Ro / Rc)^2
and
Uts / Uto = (Ro / Rs)^2

At the origin at (X = 0, Y = 0, Z = 0) the magnetic field is poloidal with the value:
Bpor = Muo Np I / 2 Ro
giving:
Upor = [Muo / 8] [Np I / Ro]^2

Due to spheromak symmetry, at the origin all the other electric and magnetic fields cancel to zero.

The ratio of:
(Bpor / Bto) = [(Muo Np I) / (2 Ro)] / [(Muo Nt I) / 2 Pi Ro]
= [(Np Pi) / Nt].

Hence the ratio:
[Upor / Uto] = [(Np Pi) / Nt]^2

However, in a spheromak the ratio (Np / Nt) can mathematically be either (~ 1 / 2) or ~ 2. Hence the ratio [Upor / Uto] = (Pi^2 / 4) or 4 Pi^2. It appears that to form a stable spheromak this ratio is likely 4 Pi^2, corresponding to:
Np / Nt = 2
which implies:
Np = (2 Nt).
This constraint reduces the solution set.

Thus, since:
P = Np + 2 Nt
Np = 2 Nt + 1 dNp = -2 dNt
for a real (Np / Nt) value or
dNp / dNt = -2
which indicates Family A.

At the spheromak wall the field energy density is the same both inside and outside the spheromak wall. Thus at the spheromak wall:
Bt^2 / 2 Muo = Bp^2 / 2 Muo + (Epsilon/ 2) Er^2 / 2
where Bt is measured just inside the wall and Bp and Er are measured just outside the wall.

This gives the boundary condition equations:
Bts^2 / 2 Muo = Bto^2 (Ro / Rs)^2 / 2 Muo = [Bps^2 / 2 Muo] + [(Epsilono / 2) Ees^2 / 2]
Btc^2 / 2 Muo = Bto^2 (Ro / Rc)^2 / 2 Muo = Bpc^2 / 2 Muo + (Epsilono / 2) Eec^2 / 2

Recall that:
Bto = [Muo Nt I / 2 Pi Ro]
or
Bto^2 = Muo^2 [Nt I / 2 Pi Ro]^2
so that the boundary condition equations become:
(Muo / 2) [Nt I / 2 Pi Ro]^2 (Ro / Rs)^2 = [Bps^2 / 2 Muo] + [(Epsilono / 2) Ees^2 / 2]
and
(Muo / 2) [Nt I / 2 Pi Ro]^2 (Ro / Rc)^2 = Bpc^2 / 2 Muo + (Epsilono / 2) Eec^2 / 2

Hence:
(Muo / 2) [Nt I / 2 Pi Ro]^2 = (Muo / 2) [Nt / 2 Pi Ro]^2 [Qs C / 2 Pi]^2 [ 1 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2} {Nt^2 + Np^2}]

= (Muo / 2) [Nt Qs C / (2 Pi)^2 Ro]^2 [ 1 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2} {Nt^2 + Np^2}]

= (Muo / 2) [Nt Qs C / (2 Pi)^2 Ro^2]^2 [ Ro^2 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2} {Nt^2 + Np^2}]

= (Muo / 2) [(Qs C)^2 / (2 Pi Ro)^4] [ Ro^2 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2}] {Nt^2 / (Nt^2 + Np^2)}

Thus the boundary conditions become:
(Muo / 2) [(Qs C)^2 / (2 Pi Ro)^4] [ Ro^2 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2}] {Nt^2 / (Nt^2 + Np^2)} (Ro / Rs)^2
= [Bps^2 / 2 Muo] + [(Epsilono / 2) Ees^2 / 2]
or
(Muo / 2) [(Qs C)^2 / (2 Pi)^4 Rs^2] [ 1 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2}] {Nt^2 / (Nt^2 + Np^2)}
= [Bps^2 / 2 Muo] + [(Epsilono / 2) Ees^2 / 2]
and
(Muo / 2) [(Qs C)^2 / (2 Pi)^4 Rc^2] [ 1 / {[(Rs - Rc) / 2]^2 [1 / 2] + [(Rs + Rc) / 2]^2}] {Nt^2 / (Nt^2 + Np^2)}
= [Bpc^2 / 2 Muo] + [(Epsilono / 2) Eec^2 / 2]

The ratio of these two boundary conditions is:
[Rc^2 / Rs^2] = {[Bps^2 / 2 Muo] + [(Epsilono / 2) Ees^2 / 2]} / {[Bpc^2 / 2 Muo] + [(Epsilono / 2) Eec^2 / 2]}

The likely simple solution to these boundary condition equations is:
[Rc^2 / Rs^2] = [Bps^2 / 2 Muo] / [Bpc^2 / 2 Muo]
and
[Rc^2 / Rs^2] = [(Epsilono / 2) Ees^2 / 2] / [(Epsilono / 2) Eec^2 / 2] or
[Rc / Rs] = Bps / Bpc`
and
[Rc / Rs] = Ees / Eec

These two equations, in combination with the field distribution in the equatorial plane, should enable determination of Rc and Rs in terms of Ro.
 

The parameters Eec, Ees, Bpc and Bps are obtained by analysis of the fields produced by the charge and current in the imaginary ring at:
R = Ro.

An important issue is finding the ratio:
Bpc / Bpor

In the central core of the spheromak the electric field direction inside the core bends upwards so that at the origin the electric field goes to zero.

Recall that at the origin:
Bpor = Muo Np I / 2 Ro
= Muo Np Qs C / 2 Ro Lh
 

In general:
Epsilono Muo = 1 / C^2

The total field energy Ett associated with a spheromak is the integral over all space of he field energy density both inside and outside the spheromak wall.

The filament length is Lh. There is a frequency:
F = C / Lh.

It is believed that (Ett / F) = h = Planck constant h.

If true then:
Ett / F = Ett Lh / C = h

An object of the spheromak analysis is to find the value of (Ett Lh / C) from first principles and compare this value to experimental measurements of the value of h.
 

SPHEROMAK WALL POSITION:
The spheromak wall position is defined by H(R) where H is the height of the spheromak wall above the equatorial plane. R = Rc, H = Z = 0
is locus of points where the spheromak's inner wall intersects the plane Z = 0.
and:BR> R = Rs, H = Z = 0

In the general case Lt must be found by a surface line integral over the spheromak wall around the spheromak's minor axis.

An important condition for spheromak shape preservation is:
(Rs - Rc) / Ro = constant independent of Ro.
 

BOUNDARY CONDITIONS:

We need to determine the ratio of Bpor to Bpc and then the ratio of electric field energy density to magnetic field energy density on the equatorial plane.

Solving spheromak problems ultimately involves introduction of prime number theory. That theory is useless without exact solutions for Np and Nt. Hence, it is necessary to determine exact values of Np, Nt, Ut, Up and Ue. Much of this web page is devoted to exact determination of U values along the major axis of symmetry at R = 0 and on the plane at Z = 0. These values allow exact determination of spheromak boundary conditions.

ENERGY DENSITY FUNCTIONS:
Solving spheromak problems ultimately involves introduction of prime number theory. That theory is useless without exact solutions for Np and Nt. Hence, it is necessary to determine exact values of Ut, Up and Ue.

In order to precisely analyse a spheromak we need exact expressions for [Ee(R, Z)]^2 and [Bp(R,Z)]^2. These functions can be calculated at R = 0 or at Z = 0 but are more difficult to calculate elsewhere. We need to accurately determine:
Bpc, Bps, Eec and Ees for precise evaluation of the boundary conditions.
We may also need to precisely determine the spheromak wall positions Rc and Rs in order to accurately calculate Lt.
 

INSIDE THE SPHEROMAK WALL:
Inside the spheromak wall the field energy density Ut as a function of position is:
Ut = Uto [Ro / R]^2
where Uto is a constant and Ro is characteristic of the spheromak size. Note that this energy density function is cylindrically radial and that:
Uto = Ut|(R = Ro)
 

OUTSIDE THE SPHEROMAK WALL:

ON AXIS ELECTRIC FIELD ENERGY DENSITY Ue DUE TO A RING OF CHARGE:
Assume that a thin ring of radius "Ro" has net charge Qs. Then the linear charge density along the thin ring is:
Qs / (2 Pi Ro)
and an element of charge is:
dQ = [Qs / (2 Pi Ro)] dL
where dL is an element of the ring's circumferential length.

Consider a point at distance "Z" along the ring axis, where Z = 0 on the ring plane.

The electric field along distance (Ro^2 + Z^2)^0.5 due to charge dQ is:
dE =(1 / 4 Pi Epsilon) [dQ / (Ro^2 + Z^2)]
where:
Epsilon = permittivity of free space

The component of this electric field along the ring axis is:
dE = (1 / 4 Pi Epsilon) [dQ / (Ro^2 + Z^2)] cos(Theta)
where:
cos(Theta) = Z / (Ra^2 + Z^2)^0.5

The net electric field E at distance Z along the ring axis is:
E = (1 / 4 Pi Epsilon) [Qs / (Ro^2 + Z^2)] cos(Theta)
= (1 / 4 Pi Epsilon) [Qs / (Ro^2 + Z^2)] [Z / (Ro^2 + Z^2)^0.5]
= (1 / 4 Pi Epsilon) [Qs Z / (Ro^2 + Z^2)^1.5]

The electric field energy density Ue at Z = Z, R = 0 is given by:
Ue = (Epsilon / 2) E^2
= (Epsilon / 2){(1 / 4 Pi Epsilon) [Qs Z / (Ro^2 + Z^2)^1.5]}^2
= [Qs^2 / (32 Pi^2 Epsilon)] [Z^2 / (Ro^2 + Z^2)^3]
= [Mu C^2 Qs^2 / (32 Pi^2)] [Z^2 / (Ro^2 + Z^2)^3]

Note that at Z = 0 the net electric field is zero and the electric field energy density is zero.

In the far field where:
Z >> Ro
then along the ring axis in the far field:
Ue = [Qs^2 / (32 Pi^2 Epsilon)] [1 / Z^4]

Thus for Z >> Ro along the ring axis the electric field energy density Ue is proportional to (1 / Z)^4.
 

ON Z AXIS MAGNETIC FIELD ENERGY DENSITY Up DUE TO A RING OF CURRENT:
The law of Biot and Savart gives an element of magnetic field dB at a measurement point on the axis of a multi-turn ring due to an electric current Np Ih is:
dB = (Mu / 4 Pi) Np Ih dL X R / |R|^3
where:
Np Ih = poloidal current around the ring
|R| = distance from current element Np Ih dL to the measurement point
Mu = magnetic permeability of free space
dL = an element of length along the direction of electric current flow around the ring
[R / |R|] = unit vector along the direction of R

Consider a ring of radius "Ro" and an axial measurement point at distance "Z" from the current ring along the ring axis.

Then along the ring axis the net magnetic field B at the measurement point is axial and is given by:
B = [(Mu / 4 Pi) Np Ih 2 Pi Ro / (Ro^2 + Z^2)] sin(Theta)
where:
(Theta) = angle between unit vector (R / |R|) and the ring axis.

However:
sin(Theta) = Ro / (Ro^2 + Z^2)^0.5

Thus the net magnetic field B along the current ring axis due to ring current Np Ih is given by::
B = [(Mu / 4 Pi) Np Ih 2 Pi Ro / (Ro^2 + Z^2)] sin(Theta)
= [(Mu / 4 Pi) Np Ih 2 Pi Ro / (Ro^2 + Z^2)][ Ro / (Ro^2 + Z^2)^0.5]
= [(Mu Np Ih) / 2] [Ro^2 / (Ro^2 + Z^2)^1.5]

The magnetic field energy density along the ring axis at Z = Z is:
Up = Bp^2 / 2 Mu
= [(Mu Np Ih) / 2]^2 [Ro^2 / (Ro^2 + Z^2)^1.5]^2 / 2 Mu
= [Mu Np^2 Ih^2 / 8] [Ro^4 / (Ro^2 + Z^2)^3]

Thus for Z >> Ro the magnetic field energy density Um is proportional to (1 / Z)^6. Hence at large distances the magnetic field energy density becomes negligibly small as compared to the electric field energy density.

At the center of the ring where Z = 0 the magnetic field is:
Bpor = [(Mu Np Ih) / (2 Ro)

The corresponding magnetic field energy density Upor at the center of the ring is:
Upor = Bpor^2 / 2 Mu
= [Mu Np^2 Ih^2 / 8 Ro^2]

Note that Upor is the magnetic field energy density at R = 0, Z = 0 corresponding to current Np Ih circulating at R = Ro.
 

TOTAL FIELD ENERGY DENSITY ALONG THE SPHEROMAK Z AXIS:
Along the spheromak axis the total electromagnetic fieldd energy density U|(R = 0, Z) is given by:
U|(R = 0, Z) = Ue|(R = 0, Z) + Up|(R = 0, Z)
= [Mu C^2 Qs^2 / (32 Pi^2)] [Z^2 / (Ro^2 + Z^2)^3] + [Mu Np^2 Ih^2 / 8] [Ro^4 / (Ro^2 + Z^2)^3]

Recall that for a spheromak:
Ih = Qs C / Lh
or along the spheromak axis:
U|(R = 0, Z) = [Mu C^2 Qs^2 / (32 Pi^2)] [Z^2 / (Ro^2 + Z^2)^3] + [Mu Np^2 Qs^2 C^2 / 8 Lh^2] [Ro^4 / (Ro^2 + Z^2)^3]

TOTAL FIELD ENERGY DENSITY Upor AT R = 0, Z = 0
Uor = [Mu C^2 Qs^2 / (Ro^2 + Z^2)^3] {(Z^2 / 32 Pi^2) + (Ro^4 Np^2 / [8 Lh^2])}
= [Mu C^2 Qs^2 / (Ro^2)^3] {(Ro^4 Np^2 / [8 Lh^2])}
= [Mu C^2 Qs^2 / (Ro^2)] {(Np^2 / [8 Lh^2])}
as expected.
 

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

ON EQUATORIAL PLANE ELECTRIC FIELD:
Now we must solve for the on-equatorial plane electric field as a function of R.

On the Z = 0 plane:
Eez = 0
giving:
Ee^2 = Eex^2 + Eey^2
Due to system symmetry, the net electric field everywhere on the equatorial plane points radially.

Consider a point located at X = R, Y = 0

The distance from point (X,Y) to point (Xo, Yo) is:
(X - Xo)^2 + (Y - Yo)^2.

The magnitude of the electric field at (X, Y) caused by dQ is:
dE = [dQ / 4 Pi Epsilono] {1 / [(X - Xo)^2 + (Y - Yo)^2]}
= [dQ / 4 Pi Epsilono] {1 / [(R - Ro cos(Phi))^2 + (0 - Ro sin(Phi))^2]}
= [dQ / 4 Pi Epsilono] {1 / [R^2 - 2 R Ro cos(Phi) + Ro^2 cos^2(Phi) + Ro^2 sin^2(Phi)]}
= [dQ / 4 Pi Epsilono] {1 / [R^2 - 2 R Ro cos(Phi) + Ro^2]}

However:
dE^2 = dEx^2 + dEy^2

Find the electric field component parallel to the Y axis at the test point (X,0):

dEy = dE (Y - Yo) / [(X - Xo)^2 + (Y - Yo)^2]^0.5
= dE (0 - Ro sin(Phi)) / [R^2 - 2 R Ro cos(Phi) + Ro^2]^0.5
= [dQ / 4 Pi Epsilono] {1 / [R^2 - 2 R Ro cos(Phi) + Ro^2]} (0 - Ro sin(Phi)) / [R^2 - 2 R Ro cos(Phi) + Ro^2]^0.5
= [dQ / 4 Pi Epsilono] {(0 - Ro sin(Phi)) / [R^2 - 2 R Ro cos(Phi) + Ro^2]^1.5}
= [Qs d(Phi) / 8 Pi^2 Epsilono] {(0 - Ro sin(Phi)) / [R^2 - 2 R Ro cos(Phi) + Ro^2]^1.5}
= [Qs d(Phi) / 8 Pi^2 Epsilono] {(- Ro sin(Phi)) / Ro^3 [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5}
= [Qs d(Phi) / 8 Pi^2 Ro^2 Epsilono] {(- sin(Phi)) / [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5}

Recall that the point (X, Y) = (X, 0) is on the X axis. Due to system symmetry:
Ey = Integral from Phi = 0 to Phi = 2 Pi of
[Qs d(Phi) / 8 Pi^2 Ro^2 Epsilono] {(- sin(Phi)) / [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5}
= 0.
 

Find the electric field parallel to the X axis at test point (X, 0):
dEx = dE (X - Xo) / [(X - Xo)^2 + (Y - Yo)^2]^0.5
= dE {(R - Ro cos(Phi)) / [R^2 - 2 R Ro cos(Phi) + Ro^2]^0.5}
= [dQ / 4 Pi Epsilono] {1 / [R^2 - 2 R Ro cos(Phi) + Ro^2]} {(R - Ro cos(Phi)) / [R^2 - 2 R Ro cos(Phi) + Ro^2]^0.5}
= [dQ / 4 Pi Epsilono] {1 / [R^2 - 2 R Ro cos(Phi) + Ro^2]^1.5} {(R - Ro cos(Phi))}
= [Qs d(Phi) / 8 Pi^2 Epsilono] {1 / [R^2 - 2 R Ro cos(Phi) + Ro^2]^1.5} {(R - Ro cos(Phi))}
= [Qs d(Phi) / 8 Pi^2 Epsilono] {1 / Ro^3 [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5} { Ro ((R / Ro) - cos(Phi))}
= [Qs / 8 Pi^2 Ro^2 Epsilono] {[(R / Ro) - cos(Phi)] / [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5} {d(Phi)}

Due to spheromak symmetry:
dEx = dEr
which gives:
Er = Integral from Phi = 0 to Phi = 2 Pi of:
[Qs / 8 Pi^2 Ro^2 Epsilono] {[(R / Ro) - cos(Phi)] / [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5} {d(Phi)}

Hence:
Erc = Integral from Phi = 0 to Phi = 2 Pi of:
[Qs / 8 Pi^2 Ro^2 Epsilono] {[(Rc / Ro) - cos(Phi)] / [(Rc / Ro)^2 - 2 (Rc / Ro) cos(Phi) + 1]^1.5} {d(Phi)}
and
Ers = Integral from Phi = 0 to Phi = 2 Pi of:
[Qs / 8 Pi^2 Ro^2 Epsilono] {[(Rs / Ro) - cos(Phi)] / [(Rs / Ro)^2 - 2 (Rs / Ro) cos(Phi) + 1]^1.5} {d(Phi)}
 

SPECIAL CASES:
For (R / Ro) = 0:
Er = Integral from Phi = 0 to Phi = 2 Pi of:
[Qs / 8 Pi^2 Ro^2 Epsilono] {[(R / Ro) - cos(Phi)] / [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5} {d(Phi)}

= Integral from Phi = 0 to Phi = 2 Pi of:
[Qs / 8 Pi^2 Ro^2 Epsilono] {[ - cos(Phi)] {d(Phi)}

= 0

For (R / Ro) >> 1:
Integral from Phi = 0 to Phi = 2 Pi of:
[Qs d(Phi) / 8 Pi^2 Ro^2 Epsilono] {[(R / Ro) - cos(Phi)] / [(R / Ro)^2 - 2 (R / Ro) cos(Phi) + 1]^1.5}

= Integral from Phi = 0 to Phi = 2 Pi of:
[Qs d(Phi) / 8 Pi^2 Ro^2 Epsilono] {[(R / Ro)] / [(R / Ro)^2]^1.5}

= [Qs 2 Pi / 8 Pi^2 Ro^2 Epsilono] {[(R / Ro)] / [(R / Ro)^3]}
= [Qs / 4 Pi Ro^2 Epsilono] [Ro / R]^2
= [Qs / 4 Pi Epsilono R^2]
as expected.
 

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

ON EQUATORIAL PLANE MAGNETIC FIELD:
Find the on equatorial plane magnetic field as a function of R.
Bpx = 0 and Bpy = 0,
giving:
Bp^2 = Bpz^2

Current (Np I) circulates around a ring of radius Ro which is in the X,Y plane and is centered at the origin. The remote point is (X, Y) which for convenience has Y = 0. The ring has equation:
Xo^2 + Yo^2 = Ro^2.

On the ring:
Xo = Ro cos(Phi)
Yo = Ro sin(Phi)

dXo = - Ro sin(Phi) d(Phi)
dYo = Ro cos(Phi) d(Phi)

dL^2 = dXo^2 + dYo^2

dL = Ro d(Phi)

Unit Vector from (Xo,Yo) to (X,Y) is:
(Xo - X)x + (Yo - Y)y / [(Xo - X)^2 + (Yo - Y)^2]^0.5

dBz = {Muo Np I / 4 Pi [(Xo - X)^2 + (Yo - Y)^2]} {[ dXox + dYoy] X [(Xo - X)x + (Yo - Y)y
/ [(Xo - X)^2 + (Yo - Y)^2]^0.5

= {Muo Np I / 4 Pi [(Xo - X)^2 + (Yo - Y)^2]^1.5} {[ dXox + dYoy] X [(Xo - X)x + (Yo - Y)y

= {Muo Np I / 4 Pi [(Xo - X)^2 + (Yo - Y)^2]^1.5} {dXo (Yo - Y) z - dYo(Xo - X) z

= {Muo Np I / 4 Pi [(Ro cos(Phi) - X)^2 + (Ro sin(Phi))^2]^1.5}
{- Ro sin(Phi) d(Phi) (Ro sin(Phi)) z - Ro cos(Phi) d(Phi)(Ro cos(Phi) - X) z}

= {Muo Np I / 4 Pi [(Ro^2 cos^2(Phi) - 2 X Ro cos(Phi) + X^2 + Ro^2 sin^2(Phi)]^1.5}
{- Ro^2 sin^2(Phi) - Ro^2 cos^2(Phi) + X Ro cos(Phi)} d(Phi) z

Thus:
dBz = {Muo Np I / 4 Pi [(Ro^2 - 2 X Ro cos(Phi) + X^2]^1.5}
{- Ro^2 + X Ro cos(Phi)} d(Phi) z

Due to system symmetry R = X giving:
dBz = {Muo Np I / 4 Pi [(Ro^2 - 2 R Ro cos(Phi) + R^2]^1.5}
{- Ro^2 + R Ro cos(Phi)} d(Phi) z
= {Muo Np I / 4 Pi Ro^3 [(1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2]^1.5}
Ro^2 {- 1 + (R / Ro) cos(Phi)} d(Phi) z
dBz = {Muo Np I / 4 Pi Ro [(1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2]^1.5}
{- 1 + (R / Ro) cos(Phi)} d(Phi) z
 

Hence:
Bzc = Integral from Phi = 0 to Phi = 2 Pi of:
{Muo Np I / 4 Pi Ro [(1 - 2 (Rc / Ro) cos(Phi) + (Rc / Ro)^2]^1.5}
{- 1 + (Rc / Ro) cos(Phi)} d(Phi) z
and
Bzs = Integral from Phi = 0 to Phi = 2 Pi of:
{Muo Np I / 4 Pi Ro [(1 - 2 (Rs / Ro) cos(Phi) + (Rs / Ro)^2]^1.5}
{- 1 + (Rs / Ro) cos(Phi)} d(Phi) z
 

SPECIAL CASES:
At R = 0 this equation for Bz simplifies to:
{Muo Np I / 4 Pi Ro [(1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2]^1.5}
{- 1 + (R / Ro) cos(Phi)} d(Phi) z

= Integral from Phi = 0 to Phi = 2 Pi of:
{Muo Np I / 4 Pi Ro [1]^1.5}
{- 1} d(Phi) z

= {Muo Np I / 2 Ro}{- 1} z
as expected except for the leading negative sign.
 

For R >> Ro:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
{Muo Np I z d(Phi) / (4 Pi Ro [(1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2]^1.5)}
{- 1 + (R / Ro) cos(Phi)}

~ Integral from Phi = 0 to Phi = 2 Pi of:
{Muo Np I / (4 Pi Ro [R / Ro]^3)} {(R / Ro) cos(Phi)} d(Phi) z

~ Integral from Phi = 0 to Phi = 2 Pi of:
{Muo Np I / (4 Pi R^2)} {Ro cos(Phi)} d(Phi) z

which integrated from Phi = 0 to Phi = 2 Pi gives:
Bz|(R >> Ro) = 0
 

EQUATORIAL BOUNDARY CONDITION SUMMARY:
Uto = [Muo Nt I / 2 Pi Ro]^2 / 2 Muo
Uts = Uto (Ro / Rs)^2
Ues + Ups = Uts
Ues = [(Epsilono / 2) Ees^2]
Ees = Integral Function of (Rs / Ro)
Ups = Bps^2 / 2 Muo
Bps = Integral Function of (Rs / Ro)
Thus we need to find an Rs value that simultaneously meets all of these requirements.

Uto = [Muo Nt I / 2 Pi Ro]^2 / 2 Muo
Utc = Uto (Ro / Rc)^2
Uec + Upc = Utc
Uec = [(Epsilono / 2) Eec^2]
Eec = Integral Function of (Rc / Ro)
Upc = Bpc^2 / 2 Muo
Bpc = Integral Function of (Rc / Ro)
Thus we need to find a Rc value that simultaneously meets all of these requirements.

In each case the calculation procedure is to guess an initial value of (Rs / Ro) = 2
or
(Rc / Ro) = 0.5
and then gradually adjust (Rs / Ro) or (Rc / Ro) until there is convergence to exact values of (Rs / Ro) and (Rc / Ro).
 

CALCULATION SEQUENCE:
1) Choose initial value of (Rs / Ro);
2) Calculate trial Bps;
3) Calculate trial Ups;
4) Calculate trial Ees;
5) Calculate trial Ues;
6) Calculate trial Uts = trial Ues + trial Ups
7) Calculate target Uts = Uto (Ro /Rs)^2
8) Calculate [Trial Uts - Target Uts]
9) Adjust trial (Rs / Ro)
10) If fractional adjustment in trial (Rs / Ro) is less than 0.01% then exit.
11) Else go back to step #2.

Repeat the above calculation sequence to determine (Rc / Ro)

Calculate spheromak geometric parameter:
[(Rs / Ro) - (Rc / Ro)]

Thus we have a means of accurately determining (Rs / Ro) and (Rc / Ro) which set the end points of H(R).
 

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

VOLUMETRIC ELECTRIC FIELD ENERGY DENSITY:
To properly model a spheromak we must find an expression for Ue(R, Z). At Z = 0 the function Ue(R, Z) must simplify to the known function Ue(R, 0). At R = 0 the function Ue(R, Z) must simplify to the known function Ue(0, Z). Due to spheromak symmetry it is sufficient to find Ue on the X, Z plane. Due to spheromak symmetry the electric field components normal to the (X, Z) plane will cancel. The resulting Ue(X, Z) can then be generalized into Ue(R, Z).

Every element of ring length Ro dPhi has an element of charge dQ = (Qs / 2 Pi Ro) (Ro dPhi) that induces an element of electric field dEx, dEy, dEz at point (X, Y, Z). We must integrate over the ring to find Ex, Ey, Ez produced at point (X, Y, Z). Then the electric field energy density at point (X, Y, Z) is:
Ue(X, Y, Z) = (Epsilono / 2)(Ex^2 + Ey^2 + Ez^2).

The remote point where the fields are to be calculated is (X, Y, Z) where for calculation simplicity, Y = 0.The point on the charge ring where dQ is located is (Xo, Yo, Zo) where:
Zo = 0
Xo = Ro cos(Phi)
Yo = Ro sin(Phi)
dQ = (Qs / 2 Pi Ro)(Ro dPhi) = Qs d(Phi) / 2 Pi
The distance between dQ and the point (X, Y, Z) is:
[(Xo - X)^2 + (Yo - Y)^2 + (Zo - Z)^2]^0.5
= [(Ro cos(Phi) - X)^2 + (Ro sin(Phi))^2 + (- Z)^2]^0.5

An element of electric field dEx at (X, Y, Z) is:
dEex = dQ (Xo- X)x / {4 Pi Epsilono [(Ro cos(Phi) - X)^2 + (Ro sin(Phi))^2 + Z^2]^1.5}

An element of electric field dEy at (X, Y, Z) is:
dEey = dQ (Yo)y / {4 Pi Epsilono [(Ro cos(Phi) - X)^2 + (Ro sin(Phi))^2 + Z^2]^1.5}

An element of electric field dEz at (X, Y, Z) is:
dEez = dQ (0 - Z)z / {4 Pi Epsilono [(Ro cos(Phi) - X)^2 + (Ro sin(Phi))^2 + (Z)^2]^1.5}

Eer = Integral from Phi = 0 TO Phi = 2 Pi of:
dQ (Ro cos(Phi)- R)x / {4 Pi Epsilono [(Ro cos(Phi) - R)^2 + (Ro sin(Phi))^2 + ( Z)^2]^1.5}

= Integral from Phi = 0 TO Phi = 2 Pi of:
[Qs d(Phi) / 2 Pi] (Ro cos(Phi)- R)x / {4 Pi Epsilono [(Ro cos(Phi) - R)^2 + (Ro sin(Phi))^2 + Z^2]^1.5}
[Qs d(Phi) / 2 Pi Ro^2] (cos(Phi)- (R / Ro))x / {4 Pi Epsilono [(cos(Phi) - (R / Ro))^2 + (sin(Phi))^2 + (Z / Ro)^2]^1.5}
= Integral from Phi = 0 TO Phi = 2 Pi of:
[Qs d(Phi) / 2 Pi Ro^2] (cos(Phi)- (R / Ro))x / {4 Pi Epsilono [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5}

At R = Rm, Z = Hm:
Eer = Integral from Phi = 0 TO Phi = 2 Pi of:
[Qs d(Phi) / 8 Pi^2 Epsilono Ro^2]
[cos(Phi) - (Rm / Ro)]x / {[1 - 2 (Rm / Ro) cos(Phi) +(Rm /Ro)^2 + (Hm / Ro)^2]^1.5}
= 0

Use this equation to find (Rm /Ro) and (Hm / Ro).

Eer^2 = [(Qs / 8 Pi^2 Epsilono]^2 {Integral from Ph = 0 to Phi = 2 Pi of:
d(Phi) (Ro cos(Phi) - R) / [(Ro cos(Phi) - R)^2 + (Ro sin(Phi))^2 + Z^2]^1.5}^2

= [(Qs / 8 Pi^2 Epsilono]^2 {Integral from Ph = 0 to Phi = 2 Pi of:
d(Phi) (Ro cos(Phi) - R) / [Ro^2 - 2 R Ro cos(Phi) + R^2 + Z^2]^1.5}^2

Note that at Z = 0 this expression simplifies to the equatorial plane solution.
 

Similarly:
Eez = Integral from Phi = 0 to Phi= 2 Pi of:
dQ (0 - Z)z / {4 Pi Epsilono [(Ro cos(Phi) - R)^2 + (Ro sin(Phi))^2 + Z^2]^1.5}
= Integral from Phi = 0 to Phi = 2 Pi of:
(Qs / 8 Pi^2 Epsilono)d(Phi)( - Z)z / [(Ro^2 - 2 R cos(Phi) + R^2 + Z^2]^1.5
= Integral from Phi = 0 to Phi = 2 Pi of:
(Qs / 8 Pi^2 Epsilono Ro^2) d(Phi)(- Z / Ro)z / [(1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5
Eez^2 = [(Qs / 8 Pi^2 Epsilono Ro^2)^2 {Integral from Phi = 0 to Phi = 2 Pi of:
d(Phi)( - Z / Ro) / [(1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5}^2

Note that at Z = 0 this term goes to zero.

Note that at R = Ro, Z = Ho this term becomes:
Eez^2|(Ro, Ho) = [(Qs / 8 Pi^2 Epsilono Ro^2)^2 {Integral from Phi = 0 to Phi = 2 Pi of:
d(Phi)( - Ho / Ro) / [(2 (1 - cos(Phi)) + (Ho / Ro)^2]^1.5}^2

To stop this integration blowing up at Phi = 0:
(Ho / Ro) > 0

Ee^2 = Eer^2 + Eez^2

Ue = (Epsilono / 2) Ee^2
 

VOLUMETRIC MAGNETIC FIELD ENERGY DENSITY:
To properly model a spheromak we must find an expression for Up(R, Z). At Z = 0 this expression must simplify to the known expresion for Up(R,0). At R = 0 this expression must simplify to the known expression for Up(0, Z). Due to spheromak symmetry it is sufficient to find Up on the (X, Z) plane. Due to spheromak symmetry the Up magnetic field components normal to the (X, Z) plane will cancel. Then Up(X, Z) can be generalized into Up(R, Z).

Now we must solve the three dimensional problem.

Every element of ring length dL has an element of current vector I dL that causes a dBx, dBy and dBz at point (X, Y, Z). We must integrate over the internal ring angle Phi to find Bx, By and Bz at point (X, Y, Z). Then the magnetic field energy density Up at point (X, Y, Z) is:
Up(X, Y, Z) = (1 / 2 Muo)(Bx^2 + By^2 + Bz^2).

The magnetic field vector expression is:
dB = [Muo Np I / 4 Pi Rr^2] (dL X [Rrx + Rry + Rrz]
where:
Rr^2 = (Xo - X)^2 + (Yo - Y)^2 + (Zo - Z)^2

A unit vector along Rr is:
Rr = Rrxx + Rryy + Rrzz
where:
Rrx = (Xo - X) / [(Xo - X)^2 + (Yo - Y)^2 + (Zo - Z)^2]^0.5
Rry = (Yo - Y) / [(Xo - X)^2 + (Yo - Y)^2 + (Zo - Z)^2]^0.5
Rrz = (Zo - Z) / [(Xo - X)^2 + (Yo - Y)^2 + (Zo - Z)^2]^0.5

Note that:
Rrx^2 + Rry^2 + Rrz^2 = 1

dL = dXox + dYoy
Xo = Ro cos(Phi)
Yo = Ro sin(Phi)
dXo = - Ro sin(Phi)d(Phi)
dYo = Ro cos(Phi) d(Phi)

I dL = = I Ro d(Phi) {- sin(Phi)x + cos(Phi)y}

CROSS PRODUCTS OF UNIT VECTORS:
x X x = 0
x X y = z
x X z = -y
y X y = 0
y X z = x
y X x = -z
z X z = 0
z X x = y
z X y = -x
dB = [Muo Np I / 4 Pi Rr^3][dL X Rr]

= [Muo Np I / 4 Pi Rr^3][dXox + dYoy] X {[(Xo - X)x + (Yo - Y)y + (Zo - Z)z]}

= [Muo Np I / 4 Pi Rr^3][dXo (Yo - Y)z - dXo (Zo - Z)y - dYo (Xo - X)z} + dYo(Zo - Z)x}]

For simplicity we choose Y = 0 and Zo = 0 to get:
dB = [Muo Np I / 4 Pi Rr^3][dXo Yoz + dXo Zy - dYo (Xo - X)z - dYo Zx]
= [Muo Np I / 4 Pi Rr^3][{dXo Yo - dYo (Xo - X)}z + dXo Zy - dYo Zx]

= [Muo Np I / 4 Pi Rr^3]d(Phi)
[(- Ro^2 sin^2(Phi) - Ro cos(Phi)(Ro cos(Phi) - X))z
- Ro sin(Phi) Zy
- Ro cos(Phi) Zx]

= [Muo Np I d(Phi) / 4 Pi Rr^3]{[- Ro^2 + Ro X cos(Phi)]z - [Ro sin(Phi) Z] y - [Ro cos(Phi) Z]x} = [Muo Np I d(Phi) Ro^2 / 4 Pi Rr^3]
{[- 1 + (X / Ro) cos(Phi)]z - [(Z / Ro) sin(Phi)] y - [(Z / Ro) cos(Phi)]x} =dBz + dBy + dBx

Recall that:
Rr^2 = (Xo - X)^2 + (Yo - Y)^2 + (Zo - Z)^2
= (Xo - X)^2 + Yo^2 + Z^2
= [Xo^2 - 2 Xo X + X^2 + Yo^2 + Z^2]
= [Ro^2 - 2 Xo X + X^2 + Z^2]
= [Ro^2 - 2 X Ro cos(Phi) + X^2 + Z^2]

Hence:
Rr^3 = [Ro^2 - 2 R Ro cos(Phi) + R^2 + Z^2]^1.5

= Ro^3 [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5

The spheromak is cylindrically symmetric. Hence the dBpy components cancel.

Then:
dBpz = [Muo Np I Ro^2 d(Phi)/ 4 Pi Rr^3][- 1 + (R / Ro)cos(Phi)] z
= [Muo Np I d(Phi) / 4 Pi Ro]
[- 1 + (R / Ro) cos(Phi)] z / [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5

Bz = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro][- 1 + (R / Ro) cos(Phi)] d(Phi)z / [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5

Along the Z axis where R = 0 the expression for Bz simplifies to:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro][- 1 ] d(Phi)z / [1 + (Z / Ro)^2]^1.5
= [Muo Np I / 4 Pi Ro][- 1 ] 2 Piz / [1 + (Z / Ro)^2]^1.5
= [Muo Np I Ro^2 / 2][- 1 ]z / [Ro^2 + Z^2]^1.5

At R = Rc, Z = 0 the expression for Bz simplifies to:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro][- 1 + (Rc / Ro) cos(Phi)] d(Phi)z / [1 - 2 (Rc / Ro) cos(Phi) + (Rc / Ro)^2]^1.5

At R = Rs, Z = 0 the expression for Bz simplifies to:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro][- 1 + (Rs / Ro) cos(Phi)] d(Phi)z / [1 - 2 (Rs / Ro) cos(Phi) + (Rs / Ro)^2]^1.5

At R = Rx, Z = Hm the expression for Bz becomes:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro]
[- 1 + (Rx / Ro) cos(Phi)] d(Phi)z / [1 - 2 (Rx / Ro) cos(Phi) + (Rx / Ro)^2 + (Hm / Ro)^2]^1.5
= 0

From the web page titled: Spheromak Structure recall that:
Hm = (Rs + Rc) / 2^0.5
and
Rx = (Rs + Rc) / 2
which together give:
Hm = 2^0.5 Rx
or
(Hm / Ro)^2 = 2 Rx^2 / Ro^2

Hence at the peak in the spheromak wall:
Integral from Phi = 0 to Phi = 2 Pi of:
[- 1 + (Rx / Ro) cos(Phi)] d(Phi) / [1 - 2 (Rx / Ro) cos(Phi) + 3 (Rx / Ro)^2]^1.5
= 0

At some value of (Rx / Ro) > 1 this equation should be satisfied. Note that:
(Ro / Ro) < (Rx / Ro) < (Rs / Ro)

Solving this integral equation gives Rx. Rx then gives Hm.

dBx = [Muo Np I d(Phi)/ 4 Pi Ro]
[- (Z / Ro) cos(Phi) x] / [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Zo)^2]^1.5

Hence:
Bx = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I d(Phi) / 4 Pi Ro][(- Z / Ro) cos(Phi) x] / [1 - 2 (R / Ro} cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5

Bx^2 = [Muo Np I / 4 Pi Ro]^2 {Integral from Phi = 0 to Phi = 2 Pi of:
[(Z / Ro) cos(Phi) d(Phi)] / [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5}^2

Note that Bx = 0 at Z = 0

The magnetic field energy density outside the spheromak wall is given by:
Up = (Bx^2 + Bz^2) / 2 Muo
 

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

BOUNDARY CONDITION AT R = Rc, Z = 0:
the boundry condition at R = Rc, Z = 0 is required to determine the ratio: Np / Nt, which in concert with the winding analysis determines K and hence other spheromak parameters such as P.
It is necesary to determine both the electric and magnetic field energy densities at R = Rc, Z = 0
and to match this data with the energy density just inside the spheromak wall at R = Rc, Z = 0. To do this matching both the electric and magnetic field energy density components on the equatorial plane need to be identified.
 

INNER FACE OF THE SPHEROMAK WALL:
Inside the spheromak wall the field energy density is given by:
Ut = Uto (Ro / R)^2
where Uto is a constant and Ro is characteristic of the spheromak size.

Let Rw be the value of R at any particular point on the spheromak wall. Then at the spheromak wall:
Ut = Utw = Uto (Ro / Rw)^2
Note that this energy density function is cylindrically radial and that:
Uto = Ut|(R = Ro)
 

Recall that:
Bto = Muo Nt I / (2 Pi Ro)
which gives:
Uto = Bto^2 / 2 Muo
= [Muo Nt I / (2 Pi Ro)]^2 / 2 Muo
= [Muo / 8][Nt I / Pi Ro]^2

Then at the spheromak wall:
Utw = Uto (Ro / Rw)^2
= [Muo / 8][Nt I / Pi Ro]^2 (Ro / Rw)^2
= [Muo / 8][Nt I / Pi Rw]^2

Recall that:
I^2 = Qs^2 C^2 / Lp^2
= Qs^2 C^2 / [(2 Pi Np Ro)^2 + (2 Pi K Ro Nt)^2]
= Qs^2 C^2 / (2 Pi Ro)^2 (Np^2 + K^2 Nt^2)

Hence:
Utw = [Muo / 8][Nt / Pi Rw]^2 [Qs^2 C^2 / (2 Pi Ro)^2 (Np^2 + K^2 Nt^2)]
= [Muo / 32 Pi^4 Rw^2 Ro^2] [Qs^2 C^2 Nt^2 / (Np^2 + K^2 Nt^2)]
= [Muo Qs^2 C^2 / 128 Pi^4][4 / Rw^2 Ro^2][Nt^2 / (Np^2 + K^2 Nt^2)]
= [Muo Qs^2 C^2 / 128 Pi^4 Ro^4][4 Ro^2 / Rw^2][Nt^2 / (Np^2 + K^2 Nt^2)]

At H = 0, Rw = Rc or Rs

The boundary condition is that at the spheromak wall:
Ut = Ue + Up
or
Utw = Uerw + Uezw + Uprw + Upzw

At (Rc, 0) and at (Rs, 0):
Uezw = 0
and
Uprw = 0

The lead constants of Uer and Uez are:
(Epsilono / 2)(Qs / 8 Pi^2 Epsilono Ro^2)^2
= Qs^2 / 128 Pi^4 Epsilono Ro^4
= Muo C^2 Qs^2 / 128 Pi^4 Ro^4

The lead constants for Upr and Upz are:
[Muo Np I / 4 Pi Ro]^2 / 2 Muo
= [Muo / 32][Np^2 I^2 / Pi^2 Ro^2
= [Muo / 32][Np^2 Qs^2 C^2 / [Ro^2 Pi^2 Lh^2]
 

FIELD ENERGY DENSITY OUTSIDE THE SPHEROMAK WALL:
The field energy density outside the spheromak wall is:
U(R, Z) = Up + Ue
= Upr + Upz + Uer + Uez
= (Br^2 + Bz^2) / 2 Muo + (Epsilono / 2)(Eer^2 + Eez^2)

At (Rc,0) and at (Rs, 0):
Br^2 = 0
and
Eez^2 = 0

Hence at (Rc, 0) and at (Rs, 0):
U = [Bz^2 / 2 Muo] + [(Epsilono / 2) Eer^2]

At (Rc, 0):
U = Uto (Ro / Rc)^2

At (Rs, 0):
U = Uto (Ro / Rs)^2

Thus we have the boundary conditions:
Uto (Ro / Rc)^2 = [Bzc^2 / 2 Muo] + [(Epsilono / 2) Eec^2]
and
Uto (Ro / Rs)^2 = [Bzs^2 / 2 Muo] + [(Epsilono / 2) Ees^2]

these two boundary condition equations must be solved to find Rc and Rs
 

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

BOUNDARY CONDITION INVOLVING Pi:
Recall that:
Upor = [Muo C Qs^2 / (16 Pi Ro^3)] {Np^2 / [Np^2 + (K Nt)^2]^0.5} {F}

Recall that:
Uto = [Muo Qs^2 C^2 / 32 Pi^4 Ro^4][Nt^2 / (Np^2 + K^2 Nt^2)]

Recall that:
F = C / Lh = C / 2 Pi Ro [Np^2 + K^2 Nt^2]^0.5
which gives:
Uto = [Muo Qs^2 C / 16 Pi^3 Ro^3][Nt^2 / (Np^2 + K^2 Nt^2)^0.5][F]

Hence:
[Upor / Uto] = [Muo C Qs^2 / (16 Pi Ro^3)] {Np^2 / [Np^2 + (K Nt)^2]^0.5} {F}
/ [Muo Qs^2 C / 16 Pi^3 Ro^3][Nt^2 / (Np^2 + K^2 Nt^2)^0.5][F]
= Pi^2 (Np / Nt)^2

Note that Np and Nt are both integers.
Np / Nt = [Upor / Uto]^0.5 / Pi
At Np = (2 Nt + 1):
Upor / Uto = [2 + (1 / Nt)]^2 Pi^2

Pi ~ 355 / 113

Pi = 355 / 113

We can get a general spheromak solution by assuming that the spheromak wall has an maximum outside diameter of Rs, an minimum inside diameter Rc. Assume that there are Nt toroidal turns and Np poloidal turns. Assume that Qs = Q = 1 charge quantum.

To solve the spheromak we need to find expressions for Ut(R), Ue(R, Z), Up(R, Z), H(R), Ett.
 

INSIDE THE SPHEROMAK WALL:
Inside the spheromak wall:
Bt = Muo Nt I / 2 Pi R
or
Bt^2 = [Muo Nt I / 2 Pi R ]^2
giving a volumetric magnetic field energy density of:
Ut = Bt^2 / 2 Muo = [Muo Nt I / 2 Pi R ]^2 / 2 Muo

The total toroidal magnetic field energy is:
Integral from R = Rc to R = Rs of:
[Bt^2 / 2 Muo] 2 Pi R dR (2 H(R))
where:
H(R) = Z value of spheromak wall at R = R.

POLOIDAL REGION:
Up + Ue has both electric field and magnetic field contributions. Both arise from an equivalent ring located at R = Ro, Z = 0

These functions will give Rs and Rc in terms of Ro.

Charge on ring is Qs. Circulating current through ring is Np I.

STRATEGY:
Find Up(R,Z) and Ue(R, Z) everywhere not on the spheromak axis
Find spheromak wall position H(R)
Do a line integral around the minor axis of the spheromak wall to find Lt
On dedicated web page Spheromak energy do volume integrals over field energy density to find Ett.
On dedicated web page address h and Fine Structure constant
On dedicated web page address spheromak magnetic moment

Charge Ring
Find E(R,Z) then Ue(R,Z)

Current Ring
Find Bp(R, Z)

Then outside the spheromak wall:
U = Ue + Up

At the spheromak wall:
Ue(R, Z) + Up(R, Z) = Ut(R) = Uto(Ro / R)^2

Spheromak energy Ett = sum of the individual volume integrals of Up + Ue + Ut

Elements of volume are cylinders centered at R = 0. The height of each elemental cylinder is set by H(R).

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

MAGNETIC FIELD ENERGY DENSITY AT R = Rc, Z = 0:
Inside the spheromak wall:
Bt = Muo Nt I / 2 Pi R
or
Bt^2 = [Muo Nt I / 2 Pi R ]^2
giving a magnetic field energy density of:
Ut = Bt^2 / 2 Muo
= [Muo Nt I / 2 Pi R ]^2 / 2 Muo
= [Muo / 8] [Nt I / Pi R]^2

At R = Rc:
Utc = Bt^2 / 2 Muo
= [Muo Nt I / 2 Pi Rc ]^2 / 2 Muo
= [Muo / 8] [Nt I / Pi Rc]^2
= [Muo / 8] [Nt Qs C / Lh Pi Rc]^2
= [Muo / 8] [Qs C / Pi Rc]^2 {Nt^2 / Lh^2}
= [Muo / 8] [Qs C / Pi Rc]^2 {Nt^2 / [(2 Pi Ro)^2 (Np^2 + K^2 Nt^2)]}
= [Muo / 32 Pi^4] [Qs C / Ro Rc]^2 [Nt^2 / (Np^2 + K^2 Nt^2)]
 

Recall that:
[1 / Ro] = 2 Pi [Np ^2 + Nt^2 K^2]^0.5 [F / C]

Hence:
Utc = [Muo / 32 Pi^4] [Qs C / Ro Rc]^2 [Nt^2 / (Np^2 + K^2 Nt^2)]

= [Muo / 32 Pi^4] [Qs^2 C^2 / Ro Rc^2] [2 Pi [Np ^2 + Nt^2 K^2]^0.5 [F / C] [Nt^2 / (Np^2 + K^2 Nt^2)]

[Muo / 16 Pi^3] [Qs^2 C / Ro Rc^2] [F] [Nt^2 / (Np^2 + K^2 Nt^2)^0.5]

= [Muo Qs^2 C / 16 Pi^3][1 / Ro Rc^2][Nt^2 / (Np^2 + K^2 Nt^2)^0.5] F
 

MAGNETIC FIELD ENERGY INSIDE THE SPHEROMAK WALL:
The total magnetic field energy inside the assumed spheromak wall is:
Integral from R = Rc to R = Rs of:
[Bt^2 / 2 Muo] 2 Pi R dR (2 H(R))

= Integral from R = Rc to R = Rs of:
[Muo / 8] [Nt I / Pi R ]^2 {4 Pi R dR}{H(R)}

= Integral from R = Rc to R = Rs of:
[Muo / 2 Pi] [Nt I]^2 [dR / R] H(R)

I^2 = Q^2 C^2 / Lh^2 = Q^2 C^2 / [(2 Pi Ro)^2 [Np^2 + Nt^2 K^2]
= Q^2 C^2 / {4 Ro^2 Pi^2 [Np^2 + K^2 Nt^2]}

Thus the total magnetic field energy inside the spheromak wall is:
Integral from R = Rc to R = Rs of:
[Muo / 2 Pi] [Nt]^2 Q^2 C^2 / {4 Ro^2 Pi^2 [Np^2 + K^2 Nt^2]}[dR / R] H(R)

= Integral from R = Rc to R = Rs of:
[Muo / 8 Pi^3] [Nt^2 Q^2 C^2 / {Ro^2 [Np^2 + K^2 Nt^2]}][dR / R] H(R)

Integral from R = Rc to R = Rs of:
[Muo Q^2 C^2 / 8 Pi^3 Ro] {Nt^2 / [Np^2 + K^2 Nt^2]} {dR H(R) / R} [1 / Ro]
 

Recall that:
[1 / Ro] = 2 Pi [Np^2 + Nt^2 K^2]^0.5 [F / C]

Hence the total magnetic field energy inside the spheromak wall is:
Integral from R = Rc to R = Rs of:
[Muo Q^2 C^2 / 8 Pi^3] {Nt^2 / [Np^2 + K^2 Nt^2]} {dR H(R) / Ro R}[1 / Ro]
 

MAGNETIC FIELD ENERGY DENSITY AT THE ORIGIN:
The magnetic field Bpor at the origin is given by:
Bpor = Muo Np I / 2 Ro
which gives:
Upor = Bpor^2 / 2 Muo
= [Muo Np I / 2 Ro]^2 / 2 Muo
= (Muo / 8) [Np I / Ro]^2
= (Muo / 8) [Np / Ro]^2 [Qs C / Lh]^2
= (Muo Qs^2 C^2 / 8)[1 / Ro]^2 [Np^2 / Lh^2]

Recall that:<
[1 / Lh^2] = 1 / [(2 Pi Ro)^2 (Np^2 + K^2 Nt^2)]
giving:
Upor = (Muo Qs^2 C^2 / 8)[1 / Ro]^2 {Np^2 / [(2 Pi Ro)^2 (Np^2 + K^2 Nt^2)]}

= (Muo Qs^2 C^2) / (32 Pi^2 Ro^3)] [Np^2 / (Np^2 + K^2 Nt^2)][1 / Ro]

= (Muo Qs^2 C^2) / (32 Pi^2 Ro^3)] [Np^2 / (Np^2 + K^2 Nt^2)] 2 Pi [Np ^2 + Nt^2 K^2]^0.5 [F / C]

(Muo Qs^2 C) / (16 Pi Ro^3)] [Np^2 / (Np^2 + K^2 Nt^2)^0.5] [F]
 

MAGNETIC FIELD ENERGY DENSITY RATIO:
[Upor / Utc] = {(Muo / 8) [Np / Ro]^2 [Qs C / Lh]^2} / {[Muo / 8] [Nt Qs C / Lh Pi Rc]^2}

= {[Np / Ro]^2} / {[Nt / Pi Rc]^2}

= (Np / Nt)^2 (Pi Rc / Ro)^2

If Upor = Utc:
then:
(Nt / Np)^2 = (Pi Rc)^2 / Ro^2
or
(Nt / Np) = (Pi Rc / Ro)

This field energy density versus distance assumption is only precisely true for an isolated spheromak in a vacuum. If a spheromak exists in regular atomic array, such as in single crystal silicon, the energy density U does not go to zero at large distances from each silicon atom. Instead at large distances the energy density rises due to the presence of other atoms in the regular crystal. This issue leads to the formation of electron energy band gaps in crystals. However, for now we will focus on isolated atomic particle spheromaks. Atomic nuclei, atoms, molecules and crystals are all more mathematically complicated due to the increased complexity of the energy density versus radial distance function.
 

SPHEROMAK ENERGY CONTENT:
The exact field energy content of a spheromak is derived on the web page titled: SPHEROMAK ENERGY.
 

The spheromak structure is consistent with the existence of stable charged particles such as electrons and protons, the Planck constant, and particle magnetic resonance. Hence the spheromak properties derived from the assumed energy distributions are the properties of real particles.

This concept can be extended to explain the behavior of electrons around an atomic nucleus. The nucleus provides the central electric field necessary to stabilize the walls of multi-electron spheromaks. As the positive nuclear charge increases the geometry of the electron spheromaks must change to meet the spheromak wall position and stability conditions. It is believed that the electron spheromaks of inert gases are exceptionally stable.

As the atomic number of an atom increases and electrons are added to the spheromaks the poloidal magnetic fields tend to cancel. Note that the conditions for existence of a multi-electron spheromak around an atomic nucleus are similar to the conditions for existence of a discrete electron or proton, so it is not surprising the both systems lead to the Planck constant.

Spheromaks can also form in plasmas, but large plasma spheromaks usually only exist for short times (< 1 ms) due to complicating factors such as neutral particle interactions with spheromak plasma particles.
 

SPHEROMAK ENERGY DENSITY GRAPHS:
Examination of the functions Up and Ut shows that at small R values Up < Ut, at medium R values Ut < Up and at large R values Up < Ut.

Shown below is a graph of Up and Ut versus R. On this graph Uto = Uo, K = 0.5 and Z = 0.5. The graph is drawn with two different ordinate scales in order to make the cross over points obvious.

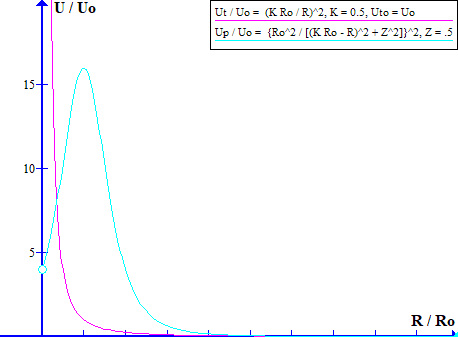
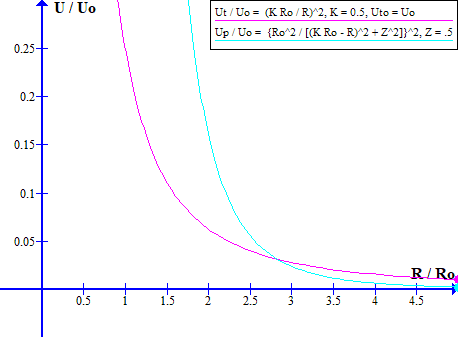
Note that in the region inside the spheromak wall the energy density is lower than it would be if the external energy density function:
Up(R, Z) = Upo {Ro^2 / [(Ro - R)^2 + Z^2}^2
took effect everywhere. Hence the spheromak forms a potential energy well. This potential energy well gives a spheromak its inherent stability.
 

In order to understand the material on this web page it is essential for the reader to study the spheromak cross sectional diagram and to identify the above mentioned parameters.
 

SPHEROMAK SHAPE:
Recall that the equation for the spheromak wall is:

The spheromak wall shape defines the surface of a toroid with a distorted cross section having a minimum inside radius Rc (core radius) and a maximum outside radius Rs. The wall position corresponds to a stable total energy minimum.

The spheromak relative shape is set by the values of the ratios (Rc / Ro), (Rs / Ro) and (Ho / Ro).
 

On the web page titled: Spheromak Structure in order to develop the spheromak winding equations it is assumed that:
(Rs - Ro) = (Ro - Rc)
and that the spheromak wall height Zw peaks at R = Ro, Zw = Ho. We need to prove these two assumptions and then calculate (Ho / Ro) before continuing to calculate (Rc / Ro) and (Rs / Ro). We should then be positioned to precisely calculate the spheromak energy integrals that are components of Ett.
 

DOES THE SPHEROMAK WALL HEIGHT PEAK AT R = Ro? THE ANSWER IS NO:
The wall height peaks at Rx = (Rs + Rc) / 2.
At the peak in spheromak wall height Bpz = 0. If this peak occurs at R = Ro then Bpz|(R = Ro) should be zero.

Recall that in the three dimensional volume:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro][- 1 + (R / Ro) cos(Phi)] d(Phi)z / [1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5

At R = Ro this expression simplifies to:
Bz = Integral from Phi = 0 to Phi = 2 Pi of:
- [Muo Np I / 4 Pi Ro][1 - cos(Phi)] d(Phi)z / [2(1 - cos(Phi)) + (Z / Ro)^2]^1.5

= Integral from Phi = 0 to Phi = 2 Pi of:
- [Muo Np I / 4 Pi Ro] d(Phi)z / [2 + {(Z / Ro)^2 / (1 - cos(Phi)}]^1.5

If we tabulate the term F = (1 - cos(Phi)) we find that:
Phi = 0 implies F = 0
Phi = Pi / 2 implies F = 1
Phi = Pi implies F = 2
Phi= 3 Pi / 2 implies F = 1
Phi = 2 Pi implies F = 0

There appears to be a mistake somewhere. Is there a sign switch at Phi= Pi?

DO Rc AND Rs BEHAVE AS ASSUMED IN THE SPHEROMAK WINDING?
We must also check the boundary conditions at (Rc,0) and at(Rs, 0). In both cases Bpr should be zero.

Furthermore, (Rs - Ro) should equal (Ro - Rc).

Bx = Integral from Phi = 0 to Phi = 2 Pi of:
[Muo Np I / 4 Pi Ro][(Z / Ro) cos(Phi) d(Phi) x] / [1 - 2 (R / Ro} cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5

At Z = 0 this term goes to zero everywhere on the equatorial plane which makes it unsuitable for defining Rc and Rs.

In order to define Rc andRs we need to match energy densies inside and outside the spheromak wall.

SPECIAL POINTS R = Ro, Z = Hm and Z = - Hm:
These points establish the top and bottom of the spheromak wall. At these points:
Ut = Uto
and the common integral denominator:
[1 - 2 (R / Ro) cos(Phi) + (R / Ro)^2 + (Z / Ro)^2]^1.5
= [2 - 2 cos(Phi) + (Z / Ro)^2]^1.5
= [2 (1 - cos(Phi)) + (Hm / Ro)^2]^1.5

Thus we can potentially solve for the spheromak parameter (Hm / Ro).

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

QUANTUM NUMBERS:
This relatively simple physical system (one quantum charge) is specified by two quantum numbers Np and Nt. There is the prime number P and there are the integers Np, Nt which indicate the energy level within P. Note that Np is constrained by the requirement that Np and Nt have no common integer factors. Note that:
dNp = - 2 dNt

It is reasonable to project that more complex physical systems will have similar mathematical structures. Chemists refer to atomic shells. Each shell will have a P value. Within each shell electron energy states will be subject to comparable Np, Nt common factor constraints. When the energy state (|Np - Npo|) in a shell becomes so large that another P value is more appropriate for that energy the system will adopt the new P value. Note that P values are constrained by a subset of the available prime numbers.

In essence energy quantization is a consequence of Np, Nt being integers. Quantization rules are primarily constraints on Np, Nt set by the existence condition that Np and Nt have no common factors. Shells are a consequence of the set of prime numbers.

Thus it appears that the electrons of an atom form multi-electron spheromak(s) around the atomic nucleus. As the atomic number of the atom is raised past an inert gas the atom's operating spheromak adopts a new P value. ie At the transition from He to Li, at the transition from Ne to Na, etc. The multi-electron spheromaks have electrons that move around the atomic nucleus in opposite directions to minimize the net poloidal atomic magnetic dipole moment while maintaining the toroidal magnetic flux. The exact geometry of this multi-electron spheromak structure has yet to be resolved.
 

This web page last updated August 16, 2024.