XYLENE POWER LTD.

PLANCK CONSTANT AND FINE STRUCTURE CONSTANT

By Charles Rhodes, P.Eng., Ph.D.

SPHEROMAK OPERATION:
A spheromak's electric and magnetic field structure allows quantized charges to act as stable packets of electro-magnetic energy. The behavior of these spheromak based energy packets is governed by the laws of electricity and magnetism. This web page shows the mathematical relationship between these laws and quantum mechanics.
 

EXPERIMENTAL OBSERVATION:
There is a change in energy dE of a particle in proportion to the frequency dF of the absorbed or emitted photon radiation in accordance with:
dE = h dF
where:
h = the Planck Constant
that has been observed in many physical experiments involving different assemblies of charged atomic particles.
 

Analysis of the Planck constant provides insight into the mechanism by which nature stores energy in rest mass and the reasons for quantum mechanical behavior.

Any physical measurement involves emission or absorption of radiant energy quanta by the system being examined. Hence there is always a potential uncertainty the equivalent of one energy quantum in the measure of any physical parameter. This issue is known as quantum uncertainty.

On Earth there is an overall tendency for incident energy carried by solar radiation to be absorbed by matter. That energy is later re-emitted from Earth by lower frequency infrared radiation which is characteristic of the surface temperature of the matter. This absorption of solar radiation and subsequent emission of infrared radiation determines the direction of evolution of many chemical reactions.
 

REST MASS ENERGY:
Matter stores energy in electromagnetic field energy configurations known as spheromaks. A spheromak has a closed current path with net charge that has associated with it both electic and magnetic fields. The length Lh of this closed current path involves many toroidal and poloidal turns and hence is long compared to the spheromak nominal radius Ro.
 

PHOTON ENERGY:
A photon is a quantum of radiant energy dE that is either emitted by or absorbed by a spheromak. To change energy a spheromak absorbs or emits photons of energy dE and frequency dFh.
 

PLANCK CONSTANT:
In interactions between matter and radiation, energy is only transferred in quantized amounts where the magnitude of the quantum of transferred energy is proportional to the emitted or absorbed photon frequency. This photon frequency Fp is equal to a change dFh in the natural particle frequency Fh.

The quantum of energy dE transferred between rest mass and the electromagnetic radiation with frequency dFh is set via the relationship:
h = dEtt / dFh
where:
h = a proportionality factor known as the Planck Constant.

This quantum of electromagnetic radiation is known as a photon.
 

HISTORICAL ORIGIN OF THE PLANCK CONSTANT:
Historically the Planck Constant h was assumed to be a natural constant that related the energy Ep carried by a photon to the frequency Fp of that photon via the formula:
Ep = h Fp
However, that formula by itself gave no insight as to the underlying mechanisms.
 

RADIATION AND MATTER:
Atomic quantum charged particles have associated electro-magnetic spheromaks. Electro-magnetic spheromaks are stable energy states. These stable states are reached by emission or absorption of radiation. During radiant energy emission and absorption total system energy and total system momentum are conserved. Charged particles and radiation, both have characteristic natural frequencies. During photon emission the emitting spheromak's natural frequency Fh decreases. During photon absorption the absorbing spheromak's natural frequency Fh increases.

Over time electromagnetic spheromaks in free space will absorb or emit energy until they reach a stable steady state.
At this stable state the value of (dEtt / dFh) for an electromagnetic spheromak is given by:
(dEtt / dFh) = h, where:
Fh = the natural frequency of the circulating quantum net charge that forms an electromagnetic spheromak and dFh is the frequency of a radiation emitted or absorbed.

If a spheromak's static electromagnetic field energy Ett changes from Ea to Eb and the spheromak frequency Fh changes from Fa to Fb then:
dEtt = (Ea - Eb)
= h (Fa - Fb)
= h dFh

This formula is the basis of quantum mechanics. Spheromaks form the static field structure of charged particles with rest mass. Since spheromaks are the main sources and sinks of radiant energy, spheromak properties in large measure determine the radiant energy absorption and emission properties of matter.
 

PLANCK CONSTANT DERIVATION:
The Planck Constant is actually a composite of other physical constants. On this web site spheromak theory is used to derive the Planck Constant from first principles. It is shown that the Planck constant h is in part a geometrical constant known as the Fine Structure constant and is in part a function of an electron charge quantum Q, the speed of light C and the permiability of free space Muo. Energy is quantized because the structure of a stable spheromak consists of stable integer numbers of poloidal and toroidal current path filament turns that form the spheromak wall. The parameter h is constant because the spheromak energy Ett and the spheromak frequency Fh are both exactly inversely proportional to the nominal spheromak radius Ro, so the ratio:
(spheromak energy) / (spheromak frequency)
is constant independent of the spheromak nominal radius Ro.

It is helpful to express a change is spheromak energy with respect to frequency in the form:
dEtt / dFh = [dEtt / (1 / dRo)] [d(1 / Ro) / d(1 / Lh)] [d(1 / Lh) / dFh]

The web page Spheromak Winding Constraints shows that:
(Lh / 2 Pi Ro) is a spheromak geometric constant (Lh / 2 Pi Ro) so that:

Lh = (Lh / 2 Pi Ro) 2 Pi Ro
or
(1 / Ro) = (Lh / 2 Pi Ro) 2 Pi (1 / Lh)
or
d(1 / Ro) / d(1 / Lh) = (Lh / 2 Pi Ro) 2 Pi

Recall that:
1 / Lh = Fh / C
or
d(1 / Lh) / dFh = (1 / C)

Combining the above expressions gives:
dEtt / dFh = [dEtt / (1 / dRo)] [d(1 / Ro) / d(1 / Lh)] [d(1 / Lh) / dFh]
= [dEtt / (1 / dRo)] [(Lh / 2 Pi Ro) 2 Pi] [1 / C]
= [dEtt / (1 / dRo)] [(Lh / 2 Pi Ro)] [2 Pi / C]
= h
which is known as the Planck Constant

Thus determination of the Planck constant requires determination of:
[dEtt / (1 / dRo)]
and determination of:
[(Lh / 2 Pi Ro)]
 

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

It is shown herein that the static field energy Ett of a quantum charge electro-magnetic spheromak at steady state in field free space is given by:
Ett = h Fh
where:
Fh = (C / Lh)
is the natural frequency of the spheromak and h is a composite of other constants that together are generally referred to as the Planck constant. If a radiant energy photon dEtt is absorbed or emitted by the spheromak:
dEtt = h dFh
where:
dFh = Fp
is the radiation photon frequency and dEtt is the photon energy.

As shown on the web page titled: ELECTROMAGNETIC SPHEROMAK for the case of:
(dNp / dNt) = - 2
then:
[Lh / (2 Pi Ro)] = [Np P]^0.5
where P is a prime number.
The relationship between spheromak frequency Fh and the nominal spheromak radius Ro is given by:
Fh = C / Lh
= {C /[Lh / 2 Pi Ro][2 Pi Ro]}

Deriving this relationship requires knowledge of both the correct energy density functions both outside and inside the spheromak wall.

Rearranging this expression gives:
[1 / Ro] = [Lh / 2 Pi Ro] (2 Pi)] Fh / C
 

SPHEROMAK ENERGY:
As shown on the web page titled: SPHEROMAK ENERGY the electromagnetic field energy associated with a spheromak is approximately:
Efs = [Uo / 2 K] Ro^3 Pi^2
where:
Uo = [(Muo C^2 Qs^2) / (32 Pi^2 Ro^4)]
and K ~ (1 / 2).

Hence:
Ef = [Uo / 2 K] Ro^3 Pi^2
= [(Muo C^2 Qs^2) / (32 Pi^2 Ro^4)](1 / 2 K) Ro^3 Pi^2
= [(Muo C^2 Qs^2) / (64 Ro K)]

Hence:
Ef = [(Muo C^2 Qs^2) / (64 K)][1 / Ro]
= [(Muo C^2 Qs^2) / (64 K)] [Lh / 2 Pi Ro] (2 Pi)] Fh / C
= [(Muo C Qs^2 Pi) / (32 K)] Fh [Lh / 2 Pi Ro]
 

******************************************************************

****************************************************************

SPHEROMAK STABLE STATE:
Over time electromagnetic spheromaks in free space will absorb or emit radiation photons until they reach their stable steady state.
At this stable state the value of (dEtt / dFh) for an electromagnetic spheromak is given by:
(dEtt / dFh) = h, where:
Fh = the natural frequency of the circulating quantum net charge that forms an electromagnetic spheromak and dFh is the frequency of a radiation photon emitted or absorbed.
 

PLANCK CONSTANT DEVELOPMENT:
The constant h can be determined theoretically by calculation of:
h = dEtt / dFh
> = [dEtt / dRo][dRo / dFh]

Although the Planck Constant is normally defined in terms of photon properties the apparent photon energy quantization is largely due to the properties of the electromagnetic spheromaks that absorb or emit the photons.

Issues in high precision experimental measurement of the Planck Constant include suppression of external electric and magnetic fields that can distort the spheromak geometry and allowance for recoil energy. These two issues make the experimentally measured value of the Planck Constant slightly dependent on the method used for its experimental measurement. The analysis herein shows that at very high resolution the Planck constant is slightly dependent on the quantum state of the system. For example the quantum state of a free electron in a vacuum may differ slightly from the quantum state of a conduction electron in a metal. The Planck constant is normally quantified by measuring the frequency of a photon emitted or absorbed during a known step change in spheromak energy. The most accurate measurement of the Planck constant is done using an apparatus known as a Kibble balance.
 

RECOIL KINETIC ENERGY:
Due to conservation of linear momentum a small portion of a change in spheromak potential energy is converted into emitting spheromak kinetic energy instead of into photon energy. The reverse is true on photon absorption. This situation can cause a small error in experimental measurement of the Planck Constant h. Similarly thermal motion of the emitting or absorbing particle can lead to small error in the measurement of the Planck Constant. Generally precise measurements are done at low temperatures to minimize the effects of particle thermal motion.
 

CURRENT FILAMENT PATH:
Our universe is composed of a large number of closed charge filaments. Each closed charge filament contains one quantum of net electric charge, approximately 1.602 X 10^-19 coulombs which flows along the string (current path) at the speed of light C, approximately 3 X 10^8 m / s. The net charge is uniformly distributed along the charge string. In a stable charged particle at every point along the current path the electric and magnetic forces are in balance. For an isolated charged particle in a vacuum that geometry is a spheromak. Hence isolated electrons and protons have a spheromak geometry.
 

SPHEROMAK ANALYSIS STRATEGY:
The Planck Constant and its contained Fine Structure Constant naturally arise from spheromak analysis. A spheromak has Np poloidal current path windings and Nt toroidal current path windings. The numbers Np and Nt are always positive integers and due to a winding constraint are related to a prime number P by the formula:
P = Np + 2 Nt

To a good approximation:
Pi = 355 / 113.

Pi (113) = 354.99997
so that the fractional error in Pi is 3 X 10^-5 / 355 ~ 10^-7, so that the Planck Constant and Fine Structure Constant can in principle be determined with an error of about one part in 10^7.

On the web page titled: Spheromak Energy Ett is developed as a function of Ro.

 

***************************************************************

PARAMETER DEFINITIONS:
A spheromak in free space has a toroidal shape with an axis of symmetry from which the radii Rc, Rs and Rf are measured:
Rc = minimum radius of inner spheromak wall;
Rs = maximum radius of outer spheromak wall;
Zw = distance of any point on the spheromak wall from the spheromak equatorial plane;
Zm = maximum value of |Zs|
2 Zm = spheromak overall height parallel to its axis of symmetry;
Rm = spheromak wall radius at Z = Zm and at Z = - Zm;
Ro = nominal spheromak radius = radius at which a circulating line current (Np I) develops the same magnetic field at the origin as does the circulating current (Np I) within the walls of the spheromak;
Lh = spheromak current path length;
Np = integer number of poloidal current path turns contained in Lh;
Nt = integer number of quasi-toroidal current path turns contained in Lh;
Nr = Np / Nt;
Lp = 2 Pi Ro = average current path poloidal turn length;
Lt = toroidal turn length
Bpo = poloidal magnetic field strength at the center of the spheromak;
Uo = (Bpo^2 / 2 Mu) = magnetic field energy density at the center of the spheromak;
 

****************************************************************

SPHEROMAK ENERGY VERSUS NOMINAL RADIUS Ro:
Recall from the web page titled: Spheromak Energy that:
dEtt
= [Ett / Ef] [dEf]

Since [Ett / Ef] ~ 0.96:
dEtt ~ 0.96 dEf
 

********************************************************************

SPHEROMAK FREQUENCY Fh:
Each spheromak has a current path length Lh, where (Lh / 2 Pi Ro) is a constant common to all spheromaks. Thus:
Lh = (Lh / 2 Pi Ro) (2 Pi Ro)
and:
Lh Fh = C
or
Fh = C / Lh
= [C /(Lh / 2 Pi Ro)][1 / 2 Pi Ro]

Hence:
Fh = [C / (Lh / 2 Pi Ro)][1 / 2 Pi] [1 / Ro]
 

********************************************************************

SPHEROMAK ENERGY:
As shown on the web page titled: SPHEROMAK ENERGY The electromagnetic field energy associated with a spheromak is approximately:
Ef = [Uo / (2 K)] Ro^3 Pi^2

As shown on the web page: ELECTROMAGNETIC SPHEROMAK Uo is given by:
Uo = [(Muo C^2 Qs^2) / (32 Pi^2 Ro^4)]

Hence:
Ef = [Uo / 2 K] Ro^3 Pi^2 = [(Muo C^2 Qs^2) / (32 Pi^2 Ro^4)](1 / 2 K) Ro^3 Pi^2
= [(Muo C^2 Qs^2) / (64 Ro K)]

Hence:
Ef = [(Muo C^2 Qs^2) / (64 K)][1 / Ro]
= [(Muo C^2 Qs^2) / (64 K)] [Lh / 2 Pi Ro] (2 Pi)] Fh / C
= [(Muo C Qs^2 Pi) / (32 K)] Fh [Lh / 2 Pi Ro]
 

PLANCK CONSTANT:
Thus the change in static field energy Ett of a spheromak with respect to the change in frequency Fh can be expressed in the form:
h = dEtt / dFh = [Ett / Ef] [Ef / Fh] = [Ett / Ef] [(Muo C Qs^2 Pi) / (32 K)][Lh / 2 Pi Ro]
which is of the form:
Ett / Fh = h
where:
h = [Ett / Efs][Muo C Qs^2 Pi / 32 K][Lh / (2 Pi Ro)]

The parameter h is known as the Planck Constant. It is constant to the extent that the spheromak relative geometrical shape parameters are constant. Note that the relative shape parameters are independent of the spheromak characteristic radius Ro.
 

*******************************************************************

FINE STRUCTURE CONSTANT:
The Fine Structure Constant Alpha is defined by:

[1 / Alpha] = 2 h / (Muo C Q^2)
 
= [2 / (Muo C Q^2)][Ett / Ef](Lh / 2 Pi Ro) [Muo C Q^2 Pi / (32 K)]

 
= [Pi / 16 K](Lh / 2 Pi Ro)[Ett / Ef]

 
= [1 / Alpha]
where Alpha is the Fine Structure constant which is a combination of spheromak parameters:
 

The web page titled: ELECTROMAGNETIC SPHEROMAK gives:
[Lh / 2 Pi Ro] = [Np P]^0.5 = [Np (Np + 2 Nt)]^0.5

Try:
Nt = 363, Np = 361, P = 1087, [Np P]^0.5 = 626.42******
Nt = 362, Np = 363, P = 1087, [Np P]^0.5 = 628.15

The nearest primes to 1087 are 1069 and 1091.

It appears that 1087 is the governing prime.

[Lh / 2 Pi Ro]^2 = Np^2 + 2 Nt^2

Np = 367, Nt = 360 393,889
Np = 365, Nt = 361 393,867
Np = 363, Nt = 362 393,857
Np = 361, Nt = 363 393,859
Np = 359, Nt = 364 393,873
Np = 357, Nt = 365 393,889

[Lh / 2 Pi Ro]^2 is minimum at Np = 363, Nt = 362, which maximizes the spheromak energy.

The old value for Ett / Ef was ~ 0.96

The web page titled: SPHEROMAK ENERGY to do this calculation properly.

********************************************************************

**************************************************************

FINE STRUCTURE CONSTANT ISSUES:
Note that (1 / Alpha) is a function of the spheromak shape parameters So^2. Note the following:
1) The spheromak energy is proportional to (1 / Alpha). Hence the spheromak has maximum energy stability when a plot of (1 / Alpha) versus So is at a relative minimum.

Alpha^-1 is a geometric ratio measured to be:
Alphas^-1 = 137.03599915

Note that the measured value of Alpha is slightly dependent on the system quantum state that can vary depending on the system environment. For example, the quantum state of a free electron in a vacuum may differ from the quantum state of a free electron in a metal which may differ again from the quantum state of an electron in a superconductor. The quantum state is specified by two numbers, Np and Nt.
 

NUMERICAL SOLUTION:
A preliminary BASIC program solution indicated that there is a broad relative minimum in [1 / (Alpha Nt)] located at So = 2.026. When So is precisely:
So = 2.02606822 the corresponding value of (1 / Alpha) is given by:
(1 / Alpha) = 137.035999

A spheromak consists of Np poloidal turns and Nt toroidal turns. The numbers Np and Nt are both integers. The ratio:
Nr = (Np / Nt)
is a rational number.

Note that Nr is the ratio of two integers which have no common factors.

The keys to finding these equations were to recognize that to prevent spheromak collapse:
Nr = (Np / Nt)
= Np / [P - 2 Np}
as in M = 2
.

The key was to recognize that A, So and Nr behave as constants. To solve a real quantum mechanical problem we must find the Nr, P, Np and Nt values corresponding to a particular Ho / Ro value.

A change in the physical environment, such as application of a strong external magnetic field, can change the parameter A which in turn might change the integers. On this web page we are primarily concerned about spheromaks in free space. Spheromaks in an atomic, molecular or crystal environment present additional complications.
 

In atoms and in crystals there are multiple interacting particles each of which experience minor changes in parameter A. These changes lead to changes in the solutions for (Np / Nt) and So which in turn change the available energy states. Everything is governed by the aforementioned quadratic equations. If an external magnetic field is applied the quadratic generates generate two solutions close to the original stable solution. That phenomena is known as magnetic resonance.

The existence, mass and other properties of atomic particles is governed in part by the limited set of prime numbers P that simultaneously satisfy all of the aforementioned equations. Since P, Np and Nt must be integers and Np and Nt cannot share common factors the number such prime numbers and hence the number of real atomic particles is distinctly limited.

One way of investigating this entire matter is to identify values of parameter A at which spheromaks collapse and hence particles cannot exist. For a particle to exist in an atom or a crystal it must have some elbow room around its nominal parameter A value in isolation in a vacuum. Thus by identifying parameter A values where particles cannot exist we can identify ranges of the parameter A value where stable particles can exist. That is the direction of my current work.

This thinking suggests that a cause of particle instability is an environment which causes an unfavorable parameter A value. However, the opposite can also be true. For example, the life time of a neutron in a stable atomic nucleus is much longer than the lifetime of a free neutron.

At first glance an A =1.000000000 seems like an obvious solution to the above equations. However, detailed examination shows that there is a spheromak collapse at:BR> A = 1.002989071
Hence a particle which relies on A = 1.00000000 for existence is inherently unstable because its spheromak will collapse if an external field causes its parameter A to increase by only 0.3%. Certain larger parameter A values result in much more stable spheromaks.

One of the practical aspects of this formulation of quantum mechanics is that solving even simple problems requires testing numerous prime numbers in nested quadratic equations. While such tests can readily be done using a computer it is not easy to convey spheromak stability concepts to persons who lack a good understanding of mathematics.

I expect that when Np, Nt and Ho / Ro are replaced by their nominal values and then small deviations of Np, Nt and A from these nominal values are examined what will emerge is the well known Schrodinger representation of quantum mechanics. ie Conventional quantum mechanics is a linear approximation of a spheromak solution. Conventional quantum mechanics relies on common real particles having parameter A values that almost always result in stable spheromaks.
 

***********************************************************************

EXPERIMENTAL RESULTS:
The published CODATA experimentally measured value of (1 / Alpha) = 137.03599915 corresponding to:
h = 6.636070150 X 10^-34 J-s.

In this context (1 / Alpha) is calculated from Kibble (Watt) balance measurements of h. The linked wiki web site indicates that there is no known way of calculating Alpha from first principles. However, the mathematical formalism developed herein potentially provide a means of calculating the theoretical value Alpha.

***************************************************************************

RECOIL KINETIC ENERGY ERROR:
Historically h was defined as:
h = Ep / Fp where:
Ep = photon energy
and
Fp = photon frequency

In circumstances where the charged particle recoil kinetic energy is negligibly small:
Ep ~ dEtt
and
Fp ~ dFh

In reality there is a small difference between Ep and dEtt due to the charged particle recoil kinetic energy caused by the momentum of the photon. This issue of recoil momentum becomes important in very high accuracy measurements of the Planck constant h.

The recoil kinetic energy error will depend on the energy Ep of the photons used and the particle mass which is usually either an electron or an atomic nucleus.

Consider an electron with rest mass Me. The rest potential energy of the electron is:
Etta = Me C^2.

The photon energy experimentally used for determination of h by non-magnetic methods is typically of the order of:
Ep = 1 eV.

For electrons: Etta = Me C^2 = 9.1 X 10^-31 kg X (3 X 10^8 m / s)^2 X 1 eV / 1.602 X 10^-19 J
= 51.12 X 10^4 eV

Hence if h is measured via photon emission from an ionized gas and if the term:
[1 +(Ep / 2 Etta)]
is assumed to be unity we can expect an error in the experimentally determined value of h of about:
(Ep / 2 Er) = 1 eV / [2 (51.12 X 10^4 eV)]
= 1 / (102.24 X 10^4)
~ 0.978 X 10^-6

Thus the discrepency between the theoretical value of h and the experimental value of h may in part be caused by failure to properly take into account recoil kinetic energy when a spheromak emits a photon during an atomic energy transition. If this error is uncorrected the experimentally measured value of h will be slightly larger than the theoretical value of h calculated herein.

Note that the Planck Constant h value calculated herein is actually the change in spheromak static potential energy Ett with respect to a change in spheromak natural frequency. The energy carried away by the photon will be slightly less than the decrease in spheromak potential energy due to the small increase in charged particle kinetic energy on emission of a photon. This increase in charged particle kinetic energy must occur to satisfy the law of conservation of linear momentum.

This issue is also known as the Mossbauer Effect and is experimentally demonstrable via use of the doppler effect and certain nuclear energy transitions.

For precise measurement of h it is important that the participating atoms be cold to minimize error due to thermal molecular motion.

Note that an experimental measurement of h will be more precise if the particle emitting or absorbing the photon has a larger rest mass. Then the recoil momentum results in less recoil energy. This issue likely improves the resolution of medical Magnetic Resonance Imaging (MRI) equipment that relies on photon absorption and emission by protons in water. However, in that application there is still disturbance of the external magnetic fields caused by the circulating electrons of the hydrogen and oxygen atoms.
 

RECOIL KINETIC ENERGY:
In crude experimental measurements it is generally assumed that:
(Esa - Esb) = Ep = photon energy
and
(Fsa - Fab) = Fp = photon frequency

However, the Planck constant is normally evaluated by measuring the frequency of the photon emitted or absorbed during a change in spheromak energy. Due to conservation of linear momentum a small portion of the change in spheromak potential energy is converted into spheromak recoil kinetic energy instead of into photon energy. The reverse is true on photon absorption. This situation causes a small error in experimental measurement of hs.

Thus the change in particle energy is:
(Esa - Esb) = Ep + dEk
where:
dEk = particle recoil kinetic energy

Experimental measurements of the Planck constant generally actually measure the parameter:
h = (Esa - Esb) / Fp
= (Ep + dEk) / Fp
= hs + (dEk / Fp)
 

When a spheromak gains or loses potential energy by absorption or emission of a photon the spheromak transitions from state "a" with potential energy Etta and natural frequency Fha to state "b" with potential energy Ettb and natural frequency Fhb. The change in spheromak potential energy is:
(Ettb - Etta) = hs (Fhb - Fha)

When a spheromak absorbs a photon with energy Ep it also absorbs that photon's linear momentum. From Einstein's famous special relativistic relationship:
E^2 = P^2 C^2 + Mo^2 C^4
the momentum Pp of a photon with no rest mass but with energy Ep is:
Pp = Ep / C
where:
C = speed of light.
 

PHOTON ABSORPTION:
If a spheromak at rest in field free space with initial spheromak potential energy Eao absorbs a photon with energy Ep to conserve momentum the spheromak with combined total energy:
Eb = (Eao + Ep)
also acquires the photon momentum Pp. Hence after photon absorption:
Eb^2 = (Eao + Ep)^2
= Pp^2 C^2 + Ebo^2
or
(Eao + Ep)^2 = Ep^2 + Ebo^2
where Ebo is the spheromak rest potential energy after absorption of the photon.

Hence:
(Eao + Ep)^2 = Ep^2 + Ebo^2
or
Eao^2 + 2 Eao Ep = Ebo^2
or
Ebo = [Eao^2 (1 + 2 Ep / Eao)]^0.5
= Eao (1 + 2 Ep / Eao)^0.5

Hence:
(Ebo - Eao) = Eao (1 + 2 Ep / Eao)^0.5 - Eao
= Eao [(1 + (2 Ep / Eao))^0.5 - 1]
~ Eao [1 + (Ep / Eao) - [(2 Ep / Eao)^2 / 8] - 1]
= Ep - (Ep^2 / 2 Eao)
= Ep [1 - (Ep / 2 Eao)]

Hence for photon absorption:
Ep = (Ebo - Eao) / [1 - (Ep / 2 Ea)]
 

PHOTON EMISSION:
If a spheromak at rest with initial potential energy Eao emits a photon with energy Ep to conserve momentum the spheromak with the new total energy (Ea - Ep) acquires the photon momentum Pp. Hence: (Eao - Ep)^2 = Pp^2 C^2 + Ebo^2
or
(Eao - Ep)^2 = Ep^2 + Ebo^2
where Ebo is the spheromak rest mass potential energy after emission of the photon.

Hence:
(Eao - Ep)^2 = Ep^2 + Ebo^2
or
Eao^2 - 2 Eao Ep = Ebo^2
or
Ebo = [Eao^2 (1 - 2 Ep / Eao)]^0.5
= Eao (1 - 2 Ep / Eao)^0.5

Hence:
(Eao - Ebo) = Eao - Eao (1 - 2 Ep / Eao)^0.5
= Eao [1 - (1 - 2 Ep / Eao)^0.5]
~ Eao [ 1 - (1 - (Ep / Eao) - (2 Ep / Eao)^2 / 8)]
= Eao [ (Ep / Eao) + (2 Ep / Eao)^2 / 8)]
= Ep + (Ep^2 / 2 Eao)
= Ep [1 + (Ep / 2 Eao)]

Hence for photon emission:
Ep = (Ea - Eb) / [1 + (Ep / 2 Ea)]
 

EXPERIMENTAL MEASUREMENT OF h:
The Planck constant h is usually defined by:
Ep = h Fp
or
h = Ep / Fp
where:
Ep = photon energy
and
Fp = photon frequency

If the experimental methodology involves measurement of the frequency of photons emitted by spheromaks at rest the formula that should be used for determining h is:
h = (Ea - Eb) / {Fp [1 + (Ep / 2 Ea)]}
Note that on emission of a photon the change in spheromak potential energy (Ea -Eb) is slightly greater than the photon energy Ep and on photon absorption by a spheromak at rest the change in spheromak potential energy is slightly less than the photon energy Ep. These issues are further complicated by thermal motion of the particles.
 

EXPERIMENTAL ERROR:
Some high resolution experimental measurements of h rely on spectroscopic measurement of the frequency of photons emitted by excited electrons. In such experiments lab personnel often incorrectly assume that the term:
[1 +/- (Ep / 2 Ea)] = 1

However, at resolutions in measurement of h with 5 or more significant figures that assumption may be wrong and the claimed experimentally measured values of h will consistently deviate from the precise theoretically calculated value of:
h = (Eb - Ea) / (Fb - Fa).
Hence, in high resolution experimental measurements of h it is necessary to account for the charged particle recoil kinetic energy on absorption or emission of a photon.

Using spheromak theory we can precisely calculate a theoretical value for:
h = (Eb - Ea) / (Fhb - Fha)
= dEtt / dFh

Note that the spheromak spacial energy density assumptions are only truly valid in field free space, which is often not the case during many practical high precision measurements of the Planck Constant. While the spheromak internal magnetic fields are large compared to an applied laboratory magnetic field, the system is not totally distortion free. Proximity of other particles can cause interfering fields that potentially affect the measurement.
 

THERMAL MOTION:
Note that if the spheromaks are in thermal motion there is broadening of the emission and absorption frequency bands which further complicates precision measurements.
 

*********************************************************************

********************************************************

THE ELECTRON:
To grasp the basic issues involved in the Planck Constant one need look no further than an electron. It has a rest mass Me = 9.109 X 10^-31 kg and a charge Q = 1.602 X 10^-19 coul. Assuming that the rest mass Ee is due to energy contained in a spherical electric field with energy density:
U = Uo {Ro^2 / [Ro^2 + R^2]}^2
then the total energy is given by:
Ee = Integral from R = Ro to R = infinity of:
U 4 Pi R^2 dR
= Integral from R = 0 to R = infinity of:
Uo {Ro^2 / [Ro^2 + R^2]^2} 4 Pi R^2 dR
= Integral from R = 0 to R = infinity of:
Uo Ro^4 4 Pi [R^2 dR / (Ro^2 + R^2)^2]
= Uo Ro^4 4 Pi {-2 Ro^2 R / [(4 Ro^2)(R^2 + Ro^2)]}|R = infinity
+ Uo Ro^4 4 Pi (2 Ro^2 / 4 Ro^2)(2 / 2 Ro) arc tan[2 R / 2 Ro]|R = infinity
- Uo Ro^4 4 Pi {-2 Ro^2 R / [(4 Ro^2)(R^2 + Ro^2)]}|R = 0
- Uo Ro^4 4 Pi (2 Ro^2 / 4 Ro^2)(2 / 2 Ro) arc tan[2 R / 2 Ro]|R = 0
 
= Uo Ro^4 4 Pi (2 Ro^2 / 4 Ro^2)(2 / 2 Ro) (Pi / 2)
 
= Uo Ro^3 Pi^2

For R >> Ro the energy density is:
U = Uo [Ro^2 / (Ro^2 + R^2)]^2
~ Uo Ro^4 / R^4

Equating the two energy densities at large distances gives:
Uo Ro^4 = [Q^2 / (32 Pi^2 Epsilono)]

Hence the total electron energy Ee is:
Ee = Uo Ro^3 Pi^2
= [Uo Ro^4] [Pi^2 / Ro]
= [Q^2 / (32 Pi^2 Epsilono)][Pi^2 / Ro]
= [Q^2 / (32 Epsilono Ro)]
= [Q^2 Muo C^2 / 32 Ro]

If one assumes that the electron charge Q is concentrated in a ring of radius Ro that rotates at the speed of light C about the electron center of mass one can calculate a frequency:
Fe = C / (2 Pi Ro)
or
Ee / Fe = [Q^2 Muo C^2 / 32 Ro] / [C / 2 Pi Ro] = Q^2 Muo C Pi / 16
= (1.60217662 X 10^-19 coul)^2 X 1.25663706 × 10-6 m kg s-2 A-2 X 299 792 458 m / s X Pi / 16
= 18.988088 X 10^-37 kg m^2 / s
= 18.988088 X 10^-37 J-s

However, that calculated value for:
(Ee / Fe) = C Q^2 Muo Pi / 16
is much smaller than the experimentally measured value of the Planck constant:
h = (Ee / Fh).
= 6.62607004 × 10-34 m2 kg / s

In order for the theoretical value of (Ee / Fe) to match the experimental value of (Ee / Fh) the current path around the electron center of mass, instead of being a simple ring, must be a complex multi-turn closed path of length Lh where:
[Lh / 2 Pi Ro] = (6.62607004 × 10-34 m2 kg / s) / (18.988088 X 10^-37 J-s)
= 348.9593075

It is also necesary to assume that electromagnetic radiation interacts with an electron's field rather than with individual current path turns. The wavelength of the interacting radiation must be about 349X the apparent physical circumference of the electron.
 

This equation indicates that at a stable value of (1 / Alpha):
Np, Nt are all constant. Note that (1 / Alpha) has a characteristic value.
 

*********************************************************************

FUNDAMENTAL EQUATIONS OF QUANTUM MECHANICS:
Charged atomic particles with rest mass contain spheromaks. A spheromak is an electric current which follows a closed spiral path that traces out the shape of the wall of a toroid with an elliptical cross section. The closed current path has both has both toroidal and poloidal circulation components. The toroidal surface is referred to as the spheromak wall.

The current circulates at the speed of light. At the spheromak geometry the total field energy density just inside the spheromak wall equals the total field energy density just outside the spheromak wall. Hence the electric and magnetic forces are in balance everywhere on the spheromak wall making the spheromak physically stable. This requirement for field energy density balance leads to the spheromak boundary condition equation:
********* When two particles interact with each other their extended electric and magnetic fields overlap causing small changes in parameter A for each particle, which leads to small integer changes in Np and Nt (quantum jumps). However, if there is a large change in parameter A, such as in a particle-anti-particle interaction, then parameter A can take a value which causes a spheromak collapse, in which case the particle rest mass energy becomes a propagating photon.

In atoms and in crystals there are multiple interacting particles each of which experience minor changes in parameter A. These changes lead to changes in the solutions for (Np / Nt) and So which in turn change the available energy states. Everything is governed by the aforementioned quadratic equations. If an external magnetic field is applied the quadratic generates generate two solutions close to the original stable solution. That phenomena is known as magnetic resonance.

The existence, mass and other properties of atomic particles is governed in part by the limited set of prime numbers P that simultaneously satisfy all of the aforementioned equations. Since P, Np and Nt must be integers and Np and Nt cannot share common factors the number such prime numbers and hence the number of real atomic particles is distinctly limited.

One way of investigating this entire matter is to identify values of parameter A at which spheromaks collapse and hence particles cannot exist. For a particle to exist in an atom or a crystal it must have some elbow room around its nominal parameter A value in isolation in a vacuum. Thus by identifying parameter A values where particles cannot exist we can identify ranges of the parameter A value where stable particles can exist. That is the direction of my current work.
 

PREFERRED ENERGY STATE:
The value of:
So^2 = 4.115
is almost coincident with the observed geometry of plasma spheromaks. Hence experimental plasma data strongly points to M = (1 / 2). M = (1 / 2) results in significantly larger So^2 values and hence lower spheromak energies than M = 2. Hence in real life M = (1 / 2) is much more energy probable than M = 2. However, M = 2 results in a higher density of states, which in certain circumstances may outweigh simple energy issues.
 

The above are the fundamental equations of quantum mechanics that must be solved in any physical situation to find Nr, P, Np and Nt. With those values, one can solve for (1 / Alpha) which leads to the Planck constant.

SUMMARY:
We have three relevant equations:
(1 / Alpha) = 137.03599915

Compare the calculated value of (1 / Alpha) to the precise experimentally measured value of 137.03599915 corresponding to:
h = 6.636070150 X 10^-34 J-s

EXPLANATION:
Recall that:
Ett = [Muo C Qs^2 / 32 A^2] [Fh][Lh / Ro]
{4 So [ So^2 - So + 1] / [(So^2 + 1)^2]}

The spheromak total static field energy Ett is the product of two functions, a energy function:
[Muo C Qs^2 / 32 A^2][Lh / Ro] Fh
which increases with decreasing Ro:
and an energy reducing spheromak shape parameter function:
S(So) = {4 So [So^2 - So + 1] / [(So^2 + 1)^2]}
which decreases as So increases from unity.

The shape parameter function S(So) has three important properties:
a) At So = 1.0 the S(So) function value is unity;
b) At So = 1.0 [dS(So) / dSo] = 0;
b) At So = 2.0 the S(So) function value is (24 / 25);
c) At So = 2.0 the ratio:
[dS(So) / dSo] / S(So) = (- 1 / 10)

To understand the stability of So we have to understand how the spheromak boundary condition sets So.

FINE STRUCTURE CONSTANT CRUDE SOLUTION:
EXPERIMENTAL
On first inspection solving the equation for the Fine Structure Constant appears quite difficult. However, we are aided by experimental data which indicates that:
(1 / Alpha)^2 ~ (137)^2 + Pi^2
or
(1 / Alpha) ~ [(137)^2 + Pi^2]^0.5
or
(1 / Alpha) = 137.035999
 

Define:
S(So) = {[4 So] [So^2 - So + 1] / [(So^2 + 1)^2]}

Note that at So = 2 this equation simplifies and gives:
S(So) = 8 [3 / 25]
 

Note that:
(1 / Alpha) = [1 / 16 A^2][Lh / Ro] [4 So]{[ (So^2 - 1) + (2 - So)] / [(So^2 + 1)^2]}
= [1 / 16 A^2] [Lh / Ro] S(So)

Recall that:
Z = [Lh / Ro] [So / Pi]
giving:
(1 / Alpha)
= [(Pi / So) Z (1 / 16 A^2)] [4 So]{[ So^2 - So + 1] / [(So^2 + 1)^2]}
 
= [(Pi / 4 A^2) Z] {[ So^2 - So + 1] / [(So^2 + 1)^2]}
 
= [(Pi / 4 A^2) Z] {[(So^2 - 1) + (2 - So)] / [(So^2 + 1)^2]}

At So = (2 + dSo):
S(So) / 8 = (3 / 25) + {[dS(So) / dSo]|So = 2} dSo

[dS(So) / dSo] = {[(So^2 + 1)^2]{[1 / 2][So^2 - So + 1] + [So / 2][2 So - 1]}
- [So / 2] [So^2 - So + 1][2 (So^2 + 1) 2 So]}
/ [(So^2 + 1)^4]
 
= {[(So^2 + 1)]{[1 / 2][So^2 - So + 1] + [So / 2][2 So - 1]}
 

CONFINED PHOTONS:
There is yet another confusing issue. The inertial mass of electrons and protons is typically three orders of magnitude higher than the mass equivalent of the static electric and magnetic field energies of the spheromak. It appears that this extra mass energy is carried by a photon which is confined by the spheromak walls.

These confined photons each contain energy Ec given by:
Ec = h Fc

However, Ec and Fc are independent of small rapid changes in the spheromak static field parameters. Thus normally when the spheromak absorbs or emits a photon there is little or no change in the confined photon energy. The confined photon energy represents most of a particle's rest mass and is very stable. Generally the confined photon energy is only emitted on a particle/anti-particle interaction.
 

ASSUMED VALUE FOR PLANCK CONSTANT:
Under the proposed new SI units the value of the Planck Constant h is fixed at:
h = 6.62607015 X 10^-34 J-s
= 6.62607015 × 10-34 m^2 kg / s.

The reason for giving h this new value is to redefine a kilogram. However, redefining a kilogram in this manner forces new precise definitions of other parameters such as the quantum charge Q, permiability of free space Muo and permittivity of free space Epsilono based on the value of the Fine Structure constant.
 

ORIGIN OF PLANCK CONSTANT:
The parameter hs is a function of:
Muos = [2 Alphas h / Qs^2 C] = permiability of free space;
Alphas = fine structure constant;
C = speed of light in a vacuum;
Qs = 1.602176634 X 10^-19 C = proton charge;
Pi = (circumference / diameter) of a circle
= 3.141592653589793
Pi^2 = 9.869604401

The definition of the fine structure constant Alpha is:
Muo C Qs^2 = 2 h Alpha

Hence:

(Muo C Qs^2 / 4 Pi) = [Alpha h / 2 Pi]

However, there is a complication. Alpha is not constant. Alpha is a weak function of the spheromak parameter So. Alpha can only be treated as a constant in circumstances where So is reliably constant. In reality So is constant because [Lh / Ro] seeks a low energy relative minimum.

To understand the relationship of spheromak parameters to the Planck constant it is necessary to derive a closed form expression for the total electric and magnetic static field energy of a spheromak.
 

As shown on the web page titled ELECTROMAGNETIC SPHEROMAK the peak magnetic field strength Bpo at the center of a spheromak can be expressed as:
Bpo = [(Muos C Qs) / (4 Pi Ro^2)]

In order to determine the spheromak operating point for each value of So^2 find the corresponding value of Nr^2 using the common boundary condition formula:
Nr^2
= {(8 / Pi^2) - [(So^2 - 1) / (So^2 + 1)]^2} / {1 - (16 / [Pi (So^2 - 1)]^2)}
*******************************************************

Hence:
Ett = Efs {1 - [(So - 1)^2 / (So^2 + 1)]^2}
or
Ett = [(Mu C Qs^2) / (4 Pi)] [Pi^2 / 8] [Fh Nt]
[(So^2 - 1) / So] [(8 {So^4 + 2 So^2 - 1} / {(So^2 - 1)^2 (Pi^2) - (16)})^0.5]
[1 - {(So - 1)^2 / (So^2 + 1)}^2]

Ett is a function of Fh and So. Hence:
dEtt = (dEtt / dFh) dFh + (dEtt / dSo) dSo

At steady state Fh is constant so:
dFh = 0
and
Nr = (Np / Nt)
adjusts so that:
(dEtt / dSo) ~ 0

This operating point is a spheromak field energy minimum.

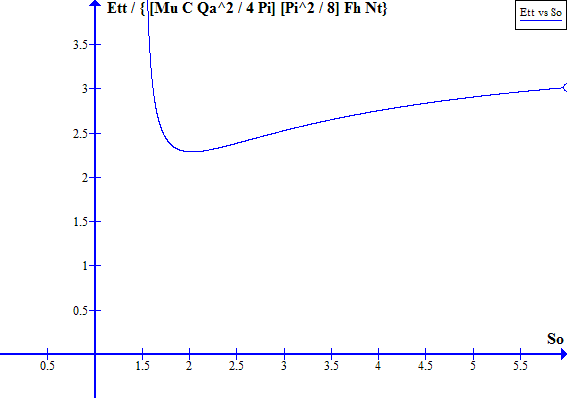
Plot:
Ett / {[Muo C Qs^2 / 4 Pi] [Pi^2 / 8] Fh Nt}
=[(So^2 - 1) / So] [(8 {So^4 + 2 So^2 - 1} / {(So^2 - 1)^2 (Pi^2) - (16)})^0.5]
[1 - {(So - 1)^2 / (So^2 + 1)}^2]
versus So to find the value of So that minimizes Ett at constant Fh. At that relative minimum:
(dEtt / dSo) = 0.

Hence at that So value:
Ett = [Muo C Qs^2 / 4 Pi] [Pi^2 / 8] Fh Nt [2.2882]

At this spheromak minimum energy operating state a small change in So causes no change in spheromak energy. At this stable operating state the spheromak energy Ett is directly proportional to the spheromak frequency Fh.

The proportionality constant h between spheromak energy Ett and frequency Fh is defined by:
h = [(Muo C Qs^2) / (4 Pi)] [Pi^2 / 8] Nt [2.2882]
and is known as the Planck Constant.

It is convenient to define the unitless Fine Structure Constant Alpha by:
[Muo C Qs^2] = 2 Alpha h

Then substitution in the above equation gives:
h = [(2 Alpha h) /(4 Pi)] [Pi^2 / 8] Nt [2.2882]
or
(1 / Alpha) = [(2) /(4 Pi)] [Pi^2 / 8] Nt [2.2882]
= [Pi / 16] Nt [2.2882]

According to this derivation:
Nt = (1 / Alpha) / {[Pi / 16][2.2882]}
= 305.00769
If this value is correct the field parameter A must be quite large.

Since by definition:
h = [Muo C Qs^2] / ( 2 Alpha)
the unitless constant Alpha can be determined from the Planck Constant.

Experimental measurements of the Planck Constant for stable particles indicate that:
Alpha ~ 137.03
which suggests that Nt is likely 303, 304 or 305.

SUMMARY:
Ett = [Muo C Qs^2 / 4 Pi] [Pi^2 / 8] Fh Nt [2.2882]
is the approximate low energy stable state of a charged particle spheromak.

When a spheromak is at its stable low energy state a small change in spheromak field energy Ett is almost entirely due to a corresponding small change in spheromak frequency Fh. At this low energy state the constant of proportionality between spheromak energy and spheromak frequency is:
dEtt / dFh = h
= [(Muo C Qs^2) / (4 Pi)] [Pi^2 / 8] Nt [2.2882]
= 6.626 X 10^-34 J-s
 

FINE STRUCTURE CONSTANT Alpha:
The fine structure constant Alpha is defined by:
Muo C Q^2 = 2 h Alpha
or
Muos C Q^2 = 2 h Alphas

EVALUATION OF Alpha:
Recall that h is given by:
h = [(Muo C Qs^2) / (4 Pi)] [Pi^2 / 8] Nt
X {1 - [(So -1)^2 / (So^2 + 1)] + [2 So (So - 1)^2 / (So^2 + 1)^2]}
X {[Nr^2 (So^2 + 1)^2] + [(So^2 - 1)]^2}^0.5 / [So]

Evaluation of the terms of hs gives:
[(Muo C Qs^2) / (4 Pi)] [Pi^2 / 8] Nt
= [Alpha h / 2 Pi] [Pi^2 / 8] Nt
= [Alphas h Pi / 16] Nt
 

At (1 / Alpha) = 137.035999:
So = 2.02606822
and
So^2 = 4.104937443
and
Nr = (Np / Nt)
= (223 / 303) = 0.7359735974
and
Nr^2 ~ 0.541657136

{1 - [(So -1)^2 / (So^2 + 1)] + [2 So (So - 1)^2 / (So^2 + 1)^2]}
= {1 - [(1.02606822)^2 / (5.104937443)] + 2 (2.02606822) [(1.02606822)^2 / (5.104937443)^2]}
= {1 - 0.2062348469 + 0.1637026404}
= 0.9574677935

{[Nr^2 (So^2 + 1)^2] + [(So^2 - 1)]^2}^0.5 / [So]
= {[0.541657136 (5.104937443)^2] + [(3.104937443)]^2}^0.5 / [2.02606822]
= {[14.1157942] + [9.640636525]}^0.5 / [2.02606822]
= 4.874056906 / [2.02606822]
= 2.405672651

Hence:
hs = [(Muos C Qs^2) / (4 Pi)] [Pi^2 / 8] Nt
X {1 - [(So -1)^2 / (So^2 + 1) + [2 So (So - 1)^2 / (So^2 + 1)^2] ]}
X {[Nr^2 (So^2 + 1)^2] + [(So^2 - 1)]^2}^0.5 / [So]

By comparison the CODATA recommended Alpha^-1 value obtained using a Kibble balance is:
Alpha^-1 = 137.03599915

The discrepency is:
(137.03599915 - 137.0355425) / 137.03599915
= 3.3 X 10^-6
 

Note that there is agreement to within 3.3 parts per million between the value of Alphas^-1 calculated herein and the CODATA recommended value of Alpha^-1 based on experimental measurements. This error is likely due to improper treatment of the parameter A.
 

It is necessary to examine exactly how h is experimentally measured with a Kibble balance to understand the discrepency sources. A possible cause of experimental to theoretical discrepency is that the spheromaks related to the Josephson junctions used with Kibble (Watt) balances are not isolated in free space.
 

CONCLUSION:
The spheromak model of a charged particle provides a means of calculating the Fine Structure Constant Alpha and hence the Planck constant h in terms of Pi, Muo, Q and C. In highly accurate experimental measurements of Alpha and h it is necessary to take into account elliptical spheromak shape distortion and the charged particle recoil kinetic energy.

Note that for a spheromak at steady state conditions in field free space Alpha is independent of the charged particle spheromak nominal radius Ro and hence is also independent of the charged particle static field energy Ett.
 

This web page last updated September 25, 2022.