| Home | Lighting Control | Micro Fusion | Electricity | Climate Change | Contacts | Links |
|---|
By Charles Rhodes, Xylene Power Ltd.
VIEW FROM OUTER SPACE:
When the earth is viewed from outer space in the thermal infrared region, what is observed are thermal emissions from molecular species that will readily interact with electromagnetic radiation. Oxygen and nitrogen do not interact with photons in the thermal emission spectrum and hence are not seen. Condensing water vapor, which emits thermal energy and which interacts with photons right across the thermal emission spectrum, is seen. For wavenumbers less than 400 cm^-1 and greater than 1300 cm^-1 high altitude water vapor obscures everything else. For wavenumbers in the range 400 cm^-1 to 1300 cm^-1 a low atmospheric water vapor concentration permits transmission of infrared radiation. However, a dense cloud will prevent infrared radiation originating below it from reaching a space vehicle above the atmosphere. Hence a space vehicle above the atmosphere sees only the top of a dense water vapor cloud and the temperature that the space vehicle sees (~270 degrees K) is the temperature of condensing water vapor near the top of the cloud.
At a wavenumber of 669 cm^-1 carbon dioxide has a much stronger absorption than water vapor. Hence, when the earth is viewed from a space vehicle through 669 cm^-1 bandpass filter the carbon dioxide in the upper atmosphere will obscure the water vapor from the space vehicle's view. At 669 cm^-1 the space vehicle sees only the very cold (~215 degrees K) CO2 in the upper atmosphere.
At a wavenumber of 1054 cm^-1 ozone in the upper atmosphere also obscures the water vapor from the space vehicle's view, so that at 1054 cm^-1 a space vehicle sees only the cold ozone in the upper atmosphere.
For other wavenumbers in the range 400 cm^-1 to 1300 cm^-1 the space vehicle can see down to the dense cloud level.
On a very clear day, when there is no cloud, the remaining water vapor is almost transparent in the region 600 cm^-1 to 1200 cm^-1. Under these circumstances within this band the space vehicle can see almost down to ground level, except within the carbon dioxide and ozone absorption bands.
TEMPERATURE WITH GREENHOUSE EFFECT:
Recall that in the Radiation Physics section it was shown that when there is no net heat absorption the average emission temperature of an element of surface area of the earth is given by:
Ta = (Ho dAc / dAs Cb)^.25[(1 - Fr) / Ft]^.25
= Te [(1 - Fr) / Ft]^.25
where emissivity Ft is measured at infrared wavelengths and albedo Fr is measured at solar wavelengths.
The infrared emission spectrum of the earth has absorption bands due to the presence of greenhouse gases. These absorption bands cause Ft to be less than unity. The temperature increase due to Ft being less than unity is known as the greenhouse effect. However, this temperature increase is partially offset by a temperature decrease due to albedo Fr being greater than zero. The local value of the albedo Fr is subject to wide variations. However, the measured average value of Fr for the entire earth, obtained from Astronomical Measurements of the Earth's Reflectance, is stable at about Fr = 0.297.
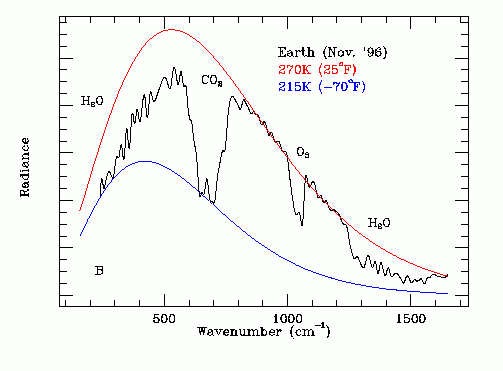
On November 23, 1996 the following Infrared Thermal Emission Spectrum of the Earth was recorded by the Mars Global Surveyor Spacecraft at a distance from earth of 4,776,000 km. The subearth point was approximately 152 degrees West longitude, 18 degrees North latitude (in the Pacific Ocean near Hawaii). The Earth filled approximately 9.3% of the Thermal Emission Spectrometer field of view.

The collection of this data is described in detail in a paper titled: "Initial data from the Mars Global Surveyor thermal emission spectrometer experiment: Observations of the Earth", JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 102, NO. E5, PAGES 10,875-10,880, MAY 25, 1997. The Thermal Emission Spectrometer apparatus used to obtain this data is described in detail in a paper titled: Mars Global Surveyor Thermal Emission Spectrometer experiment: Investigation description and surface science results", Journal of Geophysical Research, VOL. 106, NO. E10, Pages 23,823-23,871, OCTOBER 25, 2001.
The following references are applicable to the TES equipment on the Mars Global Surveyor space probe:
The Thermal Emission Spectrometer was capable of either 5 cm^-1 or 10 cm^-1 spectral resolution. We are uncertain as to the setting used for collection of this data.
On the above thermal emission graph the red black body curve represents the temperature at the top of the cloud layer over the ocean (270 K). The blue black body curve (215K) represents the temperature high in the upper atmosphere of the Earth.
Note the strong absorption band for carbon dioxide in the region 575 cm^-1 to 775 cm^-1.
Note the ozone absorption band in the region 1000 cm^-1 to 1075 cm^-1.
Note the dominant water absorption bands from 200 to 475 cm^-1 and from 1260 to 1600 cm^-1. Note the water pass band from 1600 to 1650 cm^-1. Note that there may also be methane absorption in the range 1200 cm^-1 to 1400 cm^-1 and nitrous oxide absorption in the range 1200 cm^-1 to 1350 cm^-1.
Note that in order for a spacecraft borne thermal emission spectrometer to see the ground temperature it is necessary that there be no dense clouds in its field of view. Water vapor has a sufficient broad band absorption that dense clouds are opaque in this infrared spectal range. The 270 K line corresponds to the dense cloud temperature.
Note that the data shows that the high altitude water vapor concentration plays a key role in determining emissivity Ft. This high altitude water vapor concentration will increase or decrease with the average open water surface temperature.
The ratio of the area under the thermal emission curve to the area under the 270 degrees K black body reference curve is the emissivity Ft. Scaling amplitude data off an enlarged version of this plot with a transparent plastic rule having 1 mm divisions gives:
| Wavenumber (cm^-1) | 215 K Reference | Measured Emission | 270K Reference |
|---|---|---|---|
| 0 | 0.0 | 0 | 0 |
| 50 | 0.6E | 0.6E | 0.7E |
| 100 | 1.2E | 1.2E | 1.4E |
| 150 | 2.0 | 2.0E | 2.8 |
| 200 | 3.0 | 3.0E | 4.3 |
| 250 | 3.65 | 4.1 | 5.6 |
| 300 | 4.3 | 4.9 | 7.1 |
| 350 | 4.65 | 5.9 | 7.9 |
| 400 | 4.8 | 6.3 | 8.8 |
| 450 | 4.8 | 7.3 | 9.25 |
| 500 | 4.55 | 7.8 | 9.5 |
| 550 | 4.3 | 7.7 | 9.5 |
| 600 | 3.95 | 6.3 | 9.3 |
| 650 | 3.6 | 3.6 | 9.0 |
| 700 | 3.3 | 3.3 | 8.5 |
| 750 | 2.85 | 5.2 | 8.0 |
| 800 | 2.4 | 6.7 | 7.4 |
| 850 | 2.1 | 6.5 | 6.8 |
| 900 | 1.75 | 6.2 | 6.2 |
| 950 | 1.5 | 5.6 | 5.6 |
| 1000 | 1.25 | 4.9 | 4.9 |
| 1050 | 1.05 | 3.0 | 4.4 |
| 1100 | 0.85 | 3.8 | 3.8 |
| 1150 | 0.7 | 3.3 | 3.3 |
| 1200 | 0.55 | 3.0 | 3.0 |
| 1250 | 0.40 | 2.3 | 2.55 |
| 1300 | 0.3 | 1.0 | 2.15 |
| 1350 | .25 | 1.0 | 1.85 |
| 1400 | 0.25 | 0.9 | 1.6 |
| 1450 | 0.2 | 0.7 | 1.35 |
| 1500 | 0.1 | 0.5 | 1.15 |
| 1550 | 0.1 | 0.6 | 1.0 |
| 1600 | 0.05 | 0.7 | 0.8 |
| 1650 | 0.05 | 0.7 | 0.7 |
| 1700 | 0.6E | 0.6 | |
| 1750 | 0.5E | 0.5 | |
| 1800 | 0.4E | 0.4 | |
| 1850 | 0.3E | 0.3 | |
| 1900 | 0.3E | 0.3 | |
| 1950 | 0.2E | 0.2 | |
| 2000 | 0.2E | 0.2 | |
| Column Totals: | 123.1 | 162.7 |
Hence the emissivity of the whole earth in November 1996 is given by:
Ft = 123.1 / 162.7 = .7566
Temperature Ta = 270 K from the emission spectrum plot.
Recall that for an ideal body:
Te = (Ho dAc / dAs Cb)^.25
Hence:
Ta = Te [(1 - Fr) / Ft]^.25
or
Ta / Te = [(1 - Fr) / Ft]^.25
Numerical substitution in this equation using the experimentally measured values:
Fr = .297
Ft = .7566
gives:
Ta / Te = [(1 - .297) / .7566]^.25
= .9853
Rearranging this equation gives:
Te = Ta / .9818
The experimentally measured average value of Ta is 270 degrees K, giving:
Tea = 270 K / .9818
= 275.0 K
By comparison, the theoretical value of Tea calculated in the section titled Surface Temperature of an Ideal Rotating Spherical Body is:
Tea = 278.636 K
Thus there is about a 1.2% error between theory and the results of several difficult experimental radiation measurements.
TOTAL GREENHOUSE EFFECT:
A quantity of academic interest is the difference in temperature between the Earth's present average temperature Taa and the average temperature Txa that would pertain if the planetary albedo remained constant but there was no atmospheric absorption of infrared radiation. The Earth's present average temperature Taa is given by:
Taa = Tea[(1 - Fr) / Ft]^.25
If there was no atmospheric absorption of infrared radiation, then Ft = 1, giving:
Txa = Tea[(1 - Fr)]^.25
Hence the total greenhouse effect temperature increase is:
Taa - Txa = Tea{[(1 - Fr)/Ft]^.25 - [(1 - Fr)]^.25}
Numerical substitution gives:
Taa - Txa = 278.636 k {[(1 - .297) / .7566]^.25 - [(1 - .297)]^.25}
= 278.636 {.981798 - .915669}
or
Taa - Txa = 18.426 degrees K
This web page last updated September 20, 2009
| Home | Lighting Control | Micro Fusion | Electricity | Climate Change | Contacts | Links |
|---|