CLIMATE CHANGE

RADIATION PHYSICS

By Charles Rhodes, Xylene Power Ltd.

GLOSSARY OF TERMS

THERMAL RADIATION:
All objects emit thermal electromagnetic radiation. The precise characterization of this radiation was one of the early successes of quantum mechanics.
Define:
H = 6.6256 X 10^-34 joule-sec = Planck's constant
K = 1.38054 X 10^-23 joule-K^-1 = Boltzmann constant
F = Radiation Frequency
C = 2.997925 X 10^8 m / s = speed of light
Lamda = wavelength = C / F
Pi = 3.14159
W = 2 Pi F = angular frequency

From thermal theory, the radiated power per unit area between angular frequencies W and W + dW emitted by a body with surface temperature T is given by:
P(W) dW = Ftw(W) [H / (8 Pi^3 C^2)] {W^3 dW /[exp((H W)/ (2 Pi K T)) - 1]}
where Ftw(W) is the frequency dependent emissivity
Reference: Fundamentals of Statistical and Thermal Physics by F. Reif, 1965, McGraw-Hill.

Make substitution:
Z = (H W) / (2 Pi K T)
= (H F) / (K T)
Then:
dZ = H dW /(2 Pi K T)

Rearranging these equations gives:
W = (2 Pi K T Z) / H
or
W^3 = [(2 Pi K T Z) / H]^3
and
dW = (2 Pi K T dZ) / H

Hence:
P(W) dW
= Ftw(W) [H / (8 Pi^3 C^2)] {[(2 Pi K T Z) / H]^3 [(2 Pi K T dZ) / H] /[exp(Z) - 1]}
= Ftw(W) [(2 Pi (K T)^4)/(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]

SPECIAL CASE OF Ftw(W) = CONSTANT:
For the special case of:
Ftw(W) = constant = Ft,
T = Te
then:
P(W)dW = Ft [(2 Pi (K Te)^4)/(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]
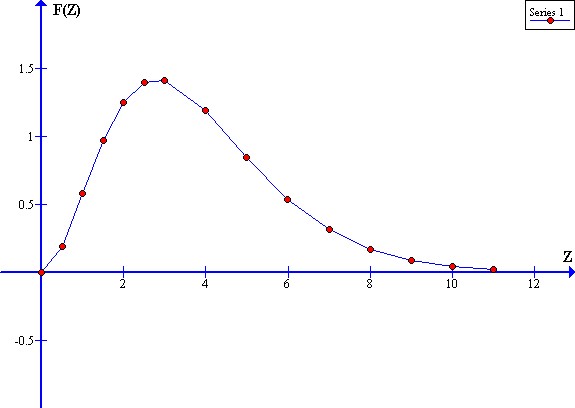
The variable component of this function is:
F(Z) = Z^3 / [exp(Z) - 1]
A graph of F(Z) versus Z gives:

This function has a power per unit frequency peak at:
Z = (H F) / (K Te) = 2.82
where:
F(Z) = [((2.82)^3) / (exp(2.82) - 1)]
= 22.425768 / 15.77685
= 1.421

About 3 / 4 of the infrared radiation power is within the range:
Z = 1.41 to Z = 5.64

For this special case of Ftw(W) = constant the total radiated power P per unit area is given by:
P = Ft [(2 Pi (KTe)^4)/(H^3 C^2)] Integral from Z = 0 to Z = infinity of:
{Z^3 dZ / [exp(Z) - 1]}
The definite integral from Z = 0 to Z = infinity of:
{Z^3 dZ / [exp(Z) - 1]}
= Pi^4 / 15
Hence:
P = Ft [(2 Pi (K Te)^4)/(H^3 C^2)][Pi^4 / 15]
= Ft (2 Pi^5) (K Te)^4/ (15 H^3 C^2)
= Ft [(2 Pi^5 K^4) / (15 H^3 C^2)] Te^4
= Ft Cb Te^4
where Cb is given by:
Cb = (2 Pi^5 K^4) / (15 H^3 C^2) = 5.6697 X 10^-8 W m^-2 K^-4 = the Stefan-Boltzmann constant.

For an ideal black body Ft = 1.

EXAMPLE (Toronto):
The wavelength of the peak in emitted power per unit frequency for an ideal body with a surface temperature of 280.06 K and Ftw(W) = constant is given by:
Lamda = C / F
= (C H) / (2.82 K Te)
= (3 X 10^8 m / s X 6.63 X 10^-34 joule-s) / (2.82 X 1.38 X 10^-23 joule-K^-1 X 280.06 K)
= .01825 X 10^-3 m
= 18.25 um
About 3 / 4 of this infrared radiation power is within the wavelength range:
Lamda = 36.5 um to Lamda = 9.1 um.

GENERAL CASE OF Ftw(W) NOT CONSTANT:
For this case:
T = Ta,
P(W) dW = Ftw(W) [(2 Pi (K Ta)^4)/(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]
In this general case the radiated power per unit area is:
P = Integral from W = 0 to W = infinity {P(W) dW}
= Integral from Z = 0 to Z = infinity of: {Ftw(W) [(2 Pi (K Ta)^4)/(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]}

If Ftw(W) = 1 the radiated power per unit area Po would be:
Po= [(2 Pi (K Ta)^4)/(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]
= Cb Ta^4

Hence Ft is given by:
Ft = P / Po
= Integral from Z = 0 to Z = infinity of:
{Ftw(W) [(2 Pi (K Ta)^4)/Cb Ta^4(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]}
= Integral from Z = 0 to Z = infinity of:
{Ftw(W) [(2 Pi (K Ta)^4)/[(2 Pi^5 K^4) / (15 H^3 C^2) ]Ta^4(H^3 C^2)] Z^3 dZ / [exp(Z) - 1]}
= Integral from Z = 0 to Z = infinity of:
{Ftw(W) [15/Pi^4] Z^3 dZ / [exp(Z) - 1]}

Thus:
Ft = Integral from Z = 0 to Z = infinity of:
{Ftw(Z) [15/Pi^4] Z^3 dZ / [exp(Z) - 1]}
where Z = (H F) / (K Ta)

For this general case:
Recall that: P / Po = Ft
and
Po = Cb Ta^4
Hence for the general case the radiated power per unit area is given by:
P = Ft Cb Ta^4

These equations relate Ft to Ftw(Z), which is the frequency or wavenumber dependent emissivity.
Note that "wavenumber" is defined by:
Wavenumber = F / C

THERMAL POWER EMITTED BY AREA dAs:
For a real body with an element of emitting surface area dAs at temperature Ta the thermal radiation emitted is:
Ft Cb Ta^4 dAs

ENERGY CONSERVATION:
Let dAc = element of Earth's cross sectional area absorbing solar radiation
Let dAs = element of Earth's surface area that emits infrared radiation energy captured by dAc
Let Ho = solar irradiance at the Earth's orbit
Let Fr = Earth's planetary albedo
Let Ha = net absorbed heat per unit surface area per unit time.
Assume that the heat conducted from the hot central core of the earth to its surface is negligibly small compared to the solar irradiance. Then energy conservation requires that:
(absorbed solar radiation) = (transmitted infrared radiation) + (net absorbed heat)
or
Ho (1 - Fr) dAc = Ft Cb Ta^4 dAs + Ha dAs
which is referred to herein as the Energy Conservation Equation. Note that Ft is measured at far infrared wavelengths and Fr is measured at solar spectrum (visible) wavelengths.

BLACK BODY MODEL:
The Energy Conservation Equation can be rewritten as:
Ho (1 - Fr) dAc = Cb Ta^4 dAs - (1 - Ft) Cb Ta^4 dAs + Ha dAs
Thus the Earth can be considered to be a black body surrounded by a reflecting filter. The incoming solar power is:
Ho dAc
of which:
Fr Ho dAc
is reflected back into space and
(1 - Fr) Ho dAc
is absorbed. The black body emits thermal radiative power is:
Cb Ta^4 dAs
of which
Ft Cb Ta^4 dAs
is transmitted into space and
(1 - Ft) Cb Ta^4 dAs
is reflected back and reabsorbed by the black body. Thus the total power absorbed by the black body is:
Ho (1 - Fr) dAc + (1 - Ft) Cb Ta^4 dAs
Energy conservation requires that this total power equals the stored thermal power
Ha dAs
plus the emitted black body radiation
Cb Ta^4 dAs
or
Ho (1 - Fr) dAc + (1 - Ft) Cb Ta^4 dAs = Ha dAs + Cb Ta^4
or
Ho (1 - Fr) dAc = Ft Cb Ta^4 dAs + Ha dAs
as before.

The importance of this black body representation is that Ta is the temperature of the equivalent black body surface where the thermal radiative emission occurs. In the case of the Earth most of the thermal radiative emission is from heat released by condensation of water vapor at cloud level, so the emission temperature Ta is the temperature at cloud level, which is less than the ground level temperature Tag. Calculations of global warming generally assume that for any point on the Earth's surface:
Tag - Ta = constant.
Typically this constant is of the order of 20 degrees C.
Then:
dTag = dTa

HEAT ABSORPTION THEORM:
The following heat absorption theorm can be used to quantify the net rate of heat absorption caused by global warming in situations where the temperature is held constant by a phase change such as the evaporation of water or the melting of ice.

The Energy Conservation Equation gives:
Ho (1 - Fr) dAc = Ft Cb Ta^4 dAs + Ha dAs
Differentiation of the Energy Conservation Equation gives:
Ho (-dFr) dAc = dFt Cb Ta^4 dAs + 4 Ft Cb Ta^3 dTa dAs + dHa dAs
for small variations in Fr, Ft, Ta and Ha.

If Ta = constant, then dTa = 0, giving:
Ho (-dFr) dAc = dFt Cb Ta^4 dAs + dHa dAs
or
dHa = [Ho (-dFr) (dAc / dAs)] - dFt Cb Ta^4

Alternatively, if Ha = constant, then dHa = 0, giving:
Ho (-dFr) dAc = dFt Cb Ta^4 dAs + 4 Ft Cb Ta^3 dTa dAs
or
Ho (-dFr) (dAc / dAs) = dFt Cb Ta^4 + (4 dTa / Ta) (Ft Cb Ta^4)

Combining the last two bold face equations gives:
dHa (for Ta = constant) = (4 dTa / Ta) (Ft Cb Ta^4) (for Ha = constant)
Substitution of the Energy Conservation Equation into this equation gives:
dHa (for Ta = constant) = (4 dTa / Ta) [(Ho (1 - Fr) (dAc / dAs) - Ha] (for Ha = constant)
For the special case of Ha = 0, this equation simplifies to:
dHa (for Ta = constant) = (4 dTa / Ta) [(Ho (1 - Fr) (dAc / dAs)] (for Ha = 0)

For a spherical Earth:
Ac = Pi R^2
As = 4 Pi R^2
Hence:
Ac / As = (1 / 4)
On average:
(dAc / dAs) = 1 / 4
giving:
dHa (for Ta = constant) = (dTa / Ta) Ho (1 - Fr) (for Ha = 0)

This equation relates the global warming induced change in heat absorption rate at constant temperature to the global warming induced change in temperature with no net heat absorption. The practical significance of this equation is that it permits calculation of dHa for polar oceans or for irrigated farm crop land from the change in average temperature dTa obtained from the Earth's thermal emission spectrum.

DRY LAND TEMPERATURE:
At dry inland locations almost all of the absorbed solar radiation is retransmitted as infrared radiation, so that:
Ha ~ 0.
Hence, rearranging the energy conservation equation gives:
Ta = (Ho dAc / dAs Cb)^.25[(1 - Fr) / Ft]^.25

TEMPERATURE OF AN IDEAL BODY:
It is helpful to first investigate the theoretical temperature Te of an ideal body with a partially reflecting surface. Assume that the reflectance Frw(W) and emissivity Ftw(W) of the surface are frequency independent. Let Te = surface temperature of this ideal body.
With frequency independent reflectance and emissivity:
Frw(W) = Fr= constant
and Ftw(W) = Ft = constant

Further assume that for this ideal body:
Ft = (1 - Fr) so Fr and Ft satisfy:
Ft + Fr = 1

Then energy balance gives: Ho dAc = Cb Te^4 dAs or
Te = (Ho dAc / Cb dAs)^.25
This is the same temperature distribution as for an ideal black body where Ft = 1 and Fr = 0.

ACTUAL EMISSION TEMPERATURE FOR Ha = 0:
For dry inland locations combining the above expressions for Ta and Te gives:
Ta = Te [(1 - Fr) / Ft]^.25
This expression shows the change in emission temperature from Te to Ta caused by non-ideal values of Fr and Ft. The emission temperature Ta is the cloud level temperature of a location on the Earth's surface, that does not absorb or emit net heat, as seen from outer space. Note that for the Earth much of the emitted thermal radiation originates at cloud level so the emission temperature Ta is generally less than the ground level temperature Tag. Most of the solar power absorption by the ocean causes evaporation which is energy and mass balanced by thermal radiative emission from the condensing water vapor, so the net heat absorption or net heat emission is relatively small.

CHANGE IN THERMAL EMISSION TEMPERATURE WHEN THERE IS NO ONGOING NET HEAT ABSORPTION:
Recall that if Ha = 0 then:
Ta = Te [(1 - Fr) / Ft]^.25
or
Ta^4 = Te^4 [(1 - Fr) / Ft]
Differentiating this expression gives:
4 Ta^3 dTa = Te^4 d[(1 - Fr) / Ft]
= Te^4 [Ft (-dFr) - (1 - Fr) dFt] / Ft^2
= Ta^4 [Ft / (1 - Fr)][(-dFr / Ft) - ((1 - Fr) dFt / Ft^2)]
= Ta^4 [(-dFr / (1 - Fr)) + (-dFt / Ft)]
or
(4 dTa / Ta) = [(-dFr / (1 - Fr)) + (-dFt / Ft)]
Recall that:
dTa = dTag
Hence:
(4 dTag / Ta) = [(-dFr / (1 - Fr)) + (-dFt / Ft)]
This equation quantifies the small change in dry inland atmospheric temperature Tag caused by small changes in Fr and Ft. Note that a decrease in Ft due to increased atmospheric CO2 concentration or increased atmospheric water vapor concentration will cause an increase in temperature. Note that an increase in Fr due to additional cloud cover will cause a partially offsetting decrease in temperature. Note that a decrease in Fr due to melting of ice will cause an increase in temperature over dry land.

Since Fr and Ft are functions of cloud cover, which varies both in time and location, the emission temperature Ta is locally highly variable. Temperature Ta will only seem to take on an average value when the whole disc or the earth is viewed so that local variations in Fr and Ft average out.

SPECIAL CASE of dFr = 0:
Experimental data seems to indicate that the planetary albedo Fr is nearly constant. Recall that:
(4 dTa / Ta) = [(-dFr / (1 - Fr)) + (-dFt / Ft)]
For the special case of dFr = 0 this equation simplifies to:
(4 dTa / Ta) = (-dFt / Ft)
or
(dTa / Ta) = (-dFt /4 Ft)
This equation relates the change in emission temperature dTa to the change in emissivity dFt when the change in planetary albedo dFr = 0.

EXACT EXPRESSION:
Assume that there is no net heat absorption or emission (Ha = 0). Then:
Ta = Te [(1 - Fr) / Ft]^.25
Assume that at some past time temperature Ta = Taa.
Assume that the present time temperature Ta = Tab.
Then:
(Tab / Taa) = [(1 - Frb) Fta / (1 - Fra) Ftb]^0.25
or
(Tab - Taa) = Taa [[(1 - Frb) Fta / (1 - Fra) Ftb]^0.25 - 1]

Note that this expression for (Tab - Taa) in terms of Taa, Fra, Frb, Fta and Ftb is exact for Ha = 0. There are no assumptions or approximations except neglecting wind. To the extent that a change in atmospheric composition affects measured values of Fr and Ft the effect of the change in atmospheric composition on Ta can be precisely calculated. However, the relationship between emission temperature Ta in the atmosphere and temperature Tag at ground level remains to be determined.

Assume that:
Tag - Ta = constant
Then:
(Tab - Taa) = (Tabg - Taag)
giving:
(Tabg - Taag) = Taa [[(1 - Frb) Fta / (1 - Fra) Ftb]^0.25 - 1]
This equation could potentially be used to evaluate future global warming if sufficiently accurate measurements of the changing values of Fr and Ft become available.

NET HEAT ABSORPTION BY THE POLAR OCEANS:
In the equitorial ocean lower density warm water floats on top of higher density cold water so the ocean surface temperature follows the average air temperature. Hence the net heat absorption rate by the equitorial ocean is relatively small.

In the polar ocean, where the ocean surface temperature is less than 4 degrees C, warming of the ocean surface water by sunlight increases its density, which makes the warmer water sink. The ocean surface temperature is effectively held constant by this effect in conjunction with the proximity of floating ice. The deep ocean heat capacity is sufficiently large that the average ocean surface temperature changes only very slowly as compared to the rate of change in atmospheric greenhouse gas concentration. Then for ocean heat absorption calculation purposes the ocean surface temperature may locally be considered constant so the heat absorption rate per unit area dHa by the polar ocean is given by:
dHa (for Ta = constant) = (dTa / Ta) Ho (1 - Fr)
where dTa is the average temperature increase at a dry inland locations as determined by analysis of the Earth's infrared emission spectrum.

Let Ap = polar ocean area
Then the rate of heat absorption by the oceans is given by:
Ap dHa = (dTa / Ta) Ho (1 - Fr) Ap
This equation, which gives the net heat absorption rate by oceans, is of importance in calculating the polar ice melting rate and hence the future rate of increase in sea level.

EXTRA IRRIGATION REQUIREMENTS:
One of the functions of farm crop irrigation is to maintain crop temperature for optimum growth and to prevent crops being damaged or destroyed on hot days. Irrigation water provides cooling by evaporation. The resulting water vapor is wind borne far from the farm before the water vapor condenses. The latent heat released during condensation contributes to the planetary infrared emission, so evaporation of irrigation water does not directly contribute to the net planetary heat absorption rate. The increase in required crop irrigation per unit time due to global warming is given by:
dHa / (Ro Hv)
where:
dHa = increase in heat absorption per crop unit area per unit time due to global warming
Ro = density of water (1000 kg / m^3)
Hv = latent heat of vaporization of water (2270 kJ / Kg)

Recall that:
dHa = (dTa / Ta) Ho (1 - Fr)
where dTa is obtained from analysis of the Earth's infrared emission spectrum.

Hence, the increase in required crop irrigation due to global warming is given by:
dHa / (Ro Hv) = (dTa / Ta) Ho (1 - Fr) / (Ro Hv)
This increase in required crop irrigation has huge practical consequences.

GLOSSARY OF TERMS

BACK NEXT

This web page last updated July 23, 2009