| Home | Lighting Control | Micro Fusion | Electricity | Climate Change | Contacts | Links |
|---|
By Charles Rhodes, Xylene Power Ltd.
INTRODUCTION:
This web page shows that doubling the atmospheric CO2 concentration from its November 1996 value of 360.76 ppmv causes a temperature increase over dry land of about 2.923 degrees C.
WARMING EQUATION:
Recall from the Radiation Physics section at radiant energy balance the Earth's emission temperature Ta seen from space is:
Ta = Te [(1 - Fr) / Ft]^.25
where:
Fr = the albedo at solar wavelengths
Ft = the emissivity at thermal infrared wavelengths
Te = theoretical average temperature defined by:
Te = (Ho dAc / dAs Cb)^.25
Due to the rotation of the earth, which causes alternating solar exposure and darkness, at any location in the Earth's atmosphere there are daily oscillations in the local atmospheric water vapor concentration. However over time these oscillations average out.
At any particular location the average temperature Te is constant as long as the solar irradiance Ho is constant and the earth's shape, axial orientation with respect to the sun and orbital path remain constant. Note that the Earth's axial orientation with respect to the sun oscillates with a period of one year.
SENSITIVITY OF Te TO Ho:
The above equation for Te can be rewritten as:
Te^4 = (Ho dAc / dAs Cb)
Differentiating gives:
4 Te^3 dTe = (dAc / dAs Cb) dHo
Divide through by Te^4 to get:
4 dTe / Te = (dAc / dAs Cb) dHo / Te^4
= (dAc / dAs Cb) dHo / (Ho dAc / dAs Cb)
= dHo / Ho
or
dTe = (Te / 4) (dHo / Ho)
Recall from the section titled Surface Temperature of an Ideal Rotating Spherical Body that for the whole Earth the effective value of Te is about 278.636 degrees K.
Recall from the section titled Solar Radiation that the variation in Ho is only +/- 3 parts in 1367 with a period of eleven years, corresponding to the sunspot cycle, giving:
dHo / Ho ~ (3 / 1367)
Thus:
dTe ~ (3 / 1367) (278.636 degrees K / 4)
= .153 degrees K
Thus natural variation in Ho associated with the eleven year sunspot cycle causes an average temperature fluctuation of about +/- 0.15 degrees C. Over the 29 year measurement period (1978 to 2007 inclusive) there was no detectable trend for the average value of Ho to either increase or decrease. Hence for the purpose of 40 year global warming trend calculations:
dTe = 0
CHANGE IN Ta DUE TO NON-AQUEOUS GREENHOUSE GASES:
For the Earth the emission temperature Ta is the temperature at the dense cloud altitude where most atmospheric water vapor condensation occurs. The emission temperature Ta can be expressed in terms of the theoretical emission temperature Te, the solar albedo Fr, and the infrared emissivity Ft.
The planetary emissivity Ft is calculated from measurements of Ftw(W) made by spacecraft as detailed in the Emissivity section.
The planetary albedo Fr can be quantified by measurement of the Earth's solar reflectivity. The average planetary albedo is a combination of the albedo of the oceans, the albedo of continents and the albedo of cloud cover. The albedo Fr is affected by ice, liquid water and water vapor but is not significantly affected by other atmospheric gases. Hence, in evaluating the effect of a relatively rapid change in atmospheric carbon dioxide concentration on Ta, Fr can be assumed to be constant. In the long term, as the ocean surface temperature increases the average atmospheric water vapor concentration will increase, causing Ft to decrease and possibly causing Fr to increase.
Consider two measurements of Ta taken at the same location with different values of Ft but with the same value of Fr (eg. atmospheric water vapor concentration is constant).
Taa = Te [(1 - Fra) / Fta]^.25
Tab = Te [(1 - Frb) / Ftb]^.25
For:
Fra = Frb
combining these two equations gives:
Tab / Taa = (Fta / Ftb)^.25
or
(Tab - Taa) = Taa[(Fta / Ftb)^.25 - 1]
which is referred to herein as the Non-aqueous Warming Equation.
This equation gives the warming (Tab - Taa) that results from a change in the concentrations of CO2 and other nonaqueous greenhouse gases in the atmosphere, provided that Fr is constant. This equation quantitatively relates non-aqueous warming (Ta2 - Ta1) to parameters that can be obtained from analysis of the earth's infrared thermal emission spectrum using the measured atmospheric carbon dioxide concentration and laboratory measurements of carbon dioxide infrared absorption. Remember that (Tab - Taa) is the non-aqueous warming at cloud level, not ground level.
The nonaqueous warming equation, together with spacecraft gathered infrared thermal emission data and laboratory measurements of gas infrared absorption data, permits calculation of the local warming due to changes in the atmospheric concentrations of carbon dioxide, methane and nitrous oxide. The remaining local warming is due to a change in average atmospheric water vapor concentration or a change in local albedo.
THERMAL EMISSION SPECTRUM:
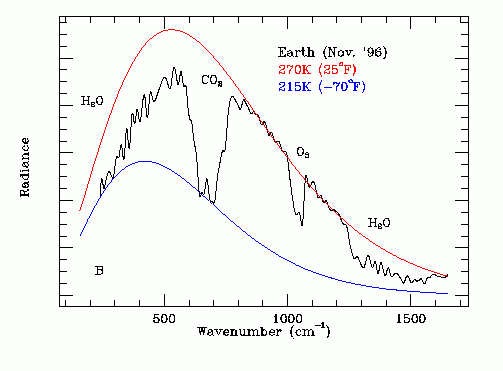
The black line on the following graph gives the experimentally measured thermal emission spectrum of the Earth as recorded by the Mars Global Surveyor space probe on November 23, 1996. Note the H2O, CO2 and O3 absorption bands. Methane (CH4) absorption is in the range 1200 cm^-1 to 1400 cm^-1. Nitrous oxide absorption is co-incident with the CO2 and CH4 absorption bands.
The area under the comparative red 270 K black body thermal emission curve and the area under the black experimentally measured thermal emission data curve were found in the Emissivity section.
Note that at frequencies (or wavenumbers) where the atmosphere is transparent to infrared radiation the red 270 K black body thermal emission curve is tangent to the black experimentally measured thermal emission data curve. Note that at frequencies (or wave numbers) where the atmosphere is opaque to infrared radiation the blue 215 K black body thermal emission curve is tangent to the black experimentally measured thermal emission data curve.
As is obvious from this graph, the largest infrared absorption is by water vapor. Water vapor determines the extent of the baseline greenhouse effect but is not directly responsible for man-made global warming. From a global warming perspective the most important greenhouse gas is carbon dioxide. However, note that CO2 related warming causes an increase in the ocean surface temperature which in turn increases the average atmospheric water vapor concentration and hence reduces Ft, causing further warming.
The relative thermal emission within the carbon dioxide absorption band versus
Wavenumber= F / C
is tabulated herein. Note that the thermal emission is low near the center of the carbon dioxide absorption band at:
Wavenumber = 669 cm^-1
and is a local maximum at the edges of the main carbon dioxide absorption band. High resolution satellite data from the period 1969 - 1971 presented in the Infrared Absorption section shows that the CO2 absorption band has a series of significant sidebands. These sidebands cause increasing global warming as the atmospheric CO2 concentration increases.
The change in Ft due to carbon dioxide is found by first determining the thermal emission spectrum that would occur with no carbon dioxide if the atmospheric water vapor concentration remained unchanged. This spectrum determination is done by copying the average relative absorbances at 40 cm^-1 wavenumber intervals from the water vapor absorption data presented in the Infrared Absorption section and then interpolating these values to obtain the relative absorbances at 50 cm^-1 intervals. The results of this interpolation are shown in the table below.
| Wavenumber | Average Measured Relative Absorbance | Interpolated Absorbance |
|---|---|---|
| 450 | 1961.7 | 1961.7 |
| 490 | 1721.9 | |
| 500 | 1479.8 | |
| 530 | 753.6 | |
| 550 | 827.1 | |
| 570 | 900.6 | |
| 600 | 667.0 | |
| 610 | 589.2 | |
| 650 | 437.0 | 437.0 |
| 690 | 465.7 | |
| 700 | 445.1 | |
| 730 | 383.2 | |
| 750 | 369.3 | |
| 770 | 355.4 | |
| 800 | 337.5 | |
| 810 | 331.5 | |
| 850 | 335.4 | 335.4 |
The absorption data at 450 cm^-1, where the direct carbon dioxide infrared absorption is negligible, is scaled using the measured Ftw(W) value and the 270 K black body value at 450 cm^-1 to calculate the Ftw(W) values and the Relative Emission values without carbon dioxide at 50 cm^-1 wavenumber intervals up to 850 cm^-1.
At 450 cm^-1:
(Relative Emission without carbon dioxide)
= (Relative emission on 270 K BB line) X exp(- absorbance X constant)
~ (Relative emission on 270 K BB line) X (1 - (absorbance X constant))
since in this region (absorbance X constant) << 1.
Rearranging this equation gives:
1 - (absorbance X constant)
= (Relative Emission without CO2) / (Relative Emission on 270 K Line)
= 7.3 / 9.25 = .7892
From above table relative absorbance at 450 nm is 1961.7. Thus:
constant = (1 - .7892) / 1961.7 = 1.074 X 10^-4
Then for other wavenumbers:
(Relative Emission without carbon dioxide)
= (Relative emission on 270 K BB line) X (1 - (absorbance X constant))
= (Relative emission on 270 K BB line) X (1 - (absorbance X 1.074 X 10^-4))
This equation is used to calculate the relative emission without carbon dioxide at 50 cm^-1 wavenumber intervals from 500 cm^-1 to 850 cm^-1.
The following table gives the wave number, the relative emission as a function of wavenumber with carbon dioxide copied from the Emissivity section for the carbon dioxide absorption band, and the relative emission without carbon dioxide obtained using the above formula:
| Wave No. (cm^-1) | Emission With CO2 | Emission Without CO2 | 270 K Black Body Emission |
|---|---|---|---|
| 450 | 7.3 | 7.301 | 9.25 |
| 500 | 7.8 | 7.990 | 9.5 |
| 550 | 7.7 | 8.656 | 9.5 |
| 600 | 6.3 | 8.634 | 9.3 |
| 650 | 3.6 | 8.578 | 9.0 |
| 700 | 3.3 | 8.094 | 8.5 |
| 750 | 5.2 | 7.683 | 8.0 |
| 800 | 6.7 | 7.132 | 7.4 |
| 850 | 6.5 | 6.555 | 6.8 |
| Column Totals: | 54.4 | 70.623 | 77.25 |
Then the difference between the Relative Emission values with and without carbon dioxide is calculated at 50 cm^-1 wavenumber intervals and integrated to find the total reduction in Relative Emission due to the concentration of carbon dioxide that pertained in November 1996. This total reduction in Relative Emission is then scaled by the total area under the 270 K black body curve to find the change in Ft due to the November 1996 concentration of carbon dioxide.
Let At = area under the 270 K black body emission curve.
The value of:
At = 162.7 is found by summing the Relative Emission values at 50 cm^-1 intervals along the comparison 270 K black body curve,as shown in the section titled Emissivity.
Let An = area reduction under the thermal emission curve due to CO2 absorption.
The change (- An / At) in Ft due to the atmospheric carbon dioxide concentration that existed in November 1996 is given by:
(An / At) = (70.623 - 54.4) / 162.7
= .0997
GREENHOUSE WARMING DIRECTLY DUE TO CARBON DIOXIDE:
Recall that with the carbon dioxide present in November 1996 we obtained the Emissivity of the Earth as:
Ftb = .7566.
Without this carbon dioxide the emissivity of the Earth would have been:
Fta = .7566 + .0997
=.8563
Without the carbon dioxide that existed in November 1996 Ta would decrease from:
Tab = 270 K
to:
Taa = Tab X (Ftb / Fta)^0.25
= (270 K) X (.7566 / .8563)^.25
= 261.77 K
Hence the greenhouse warming directly due to the atmospheric carbon dioxide concentration that existed in November 1996 was:
270 K - 261.77 K = 8.228 K
Note that this calculation assumes no accompanying change in the atmospheric concentrations of water vapor or ozone and that the nitrous oxide concentration (N2O) is negligibly small. Nitrous oxide has a narrow absorption line within the CO2 absorption band. In reality the temperature change is amplified due to an accompanying change in atmospheric water vapor concentration.
THE EFFECT OF DOUBLING THE ABSORBING GAS CONCENTRATION:
If the upper atmosphere contained no infrared absorbing gas, the upper atmosphere would be completely transparent at infrared frequencies and the emission as a function of frequency F would take the 270 K black body values, which are representative of the temperature at the dense cloud layer near the bottom of the atmosphere.
If the upper atmosphere contained a large concentration of a broadband strongly infrared absorbing gas the upper atmosphere would be opaque at infrared frequencies and the emission as a function of frequency F would take the 215 K black body values, which are representative of the temperature at the top of the atmosphere.
Let E(F) denote the emission as a function of frequency F or Wavenumber (F / C). Then:
Eh(F) = emission as a function of frequency F of a 270 K black body;
El(F) = emission as a function of frequency F of a 215 K black body;
Eb(F) = Measured emission at a measured atmospheric concentration of the absorbing gas;
Ec(F) = Projected emission at twice the measured atmospheric concentration of the absorbing gas.
The function relating the emission versus frequency E(F) within the absorbing gas absorption band to the atmospheric concentration of the absorbing gas D is subject to the following conditions:
1. When D = 0, E(F) = Eh(F);
2. E(F) decreases monotonically as D increases;
3. When D is small the decrease in E(F) is proportional to D;
4. When the absorbing gas concentration is its experimentally measured value E(F) = Eb(F);
5. When the absorbing gas concentration is twice its experimentally measured value E(F) = Ec(F);
6. When absorbing gas concentration is large: E(F) = El(F);
7. To quantify the change in temperature triggered by doubling the absorbing gas concentration the quantity [Eb(F) - Ec(F)] must be expressed in terms of readily measureable parameters.
A mathematical solution that meets all of these requirements is:
Eb(F) = Eh(F) - [1 - exp(-Co(F)D)][Eh(F) - El(F)]
where Co(F) is the absorption constant as a function of frequency F and D is the measured atmospheric absorbing gas concentration. When the atmospheric absorbing gas concentration is doubled:
Ec(F) = Eh(F) - [1 - exp(-2Co(F)D)][Eh(F) - El(F)]
Subtracting Ec from Eb gives:
Eb(F) - Ec(F) = exp(-Co(F)D)[Eh(F) - El(F)][1 - exp(-Co(F)D)]
Recall that:
Eb(F) = Eh(F) - [1 - exp(-Co(F)D)][Eh(F) - El(F)]
or
[1 - exp(-Co(F)D)] = [Eh(F) - Eb(F)] / [Eh(F) - El(F)]
or
exp(-Co(F)D) = [Eb(F) - El(F)] / [Eh(F) - El(F)]
Therefore:
Eb(F) - Ec(F) = {[Eb(F) - El(F)] / [Eh(F) - El(F)]}[Eh(F) - El(F)]{[Eh(F) - Eb(F)] / [Eh(F) - El(F)]}
= {[Eb(F) - El(F)][Eh(F) - Eb(F)]} / [Eh(F) - El(F)]
or
Eb(F) - Ec(F) = {[Eh(F) - Eb(F)][Eb(F) - El(F)]} / [Eh(F) - El(F)]
This equation can be easily evaluated for each value of F within the frequency bands where the absorbing gas is active. Hence the change in emissivity due to a sudden doubling of the absorbing gas concentration can be evaluated.
CHANGE IN EMISSIVITY DUE TO SUDDEN DOUBLING OF THE ATMOSPHERIC CO2 CONCENTRATION:
| Wavenumber (cm^-1) | El=215 K Black Body | Measured Emission Eb | Eh = Emission With No CO2 | (Eb - Ec) |
|---|---|---|---|---|
| 450 | 4.8 | 7.3 | 7.3 | 0 |
| 500 | 4.55 | 7.8 | 7.990 | .180 |
| 550 | 4.3 | 7.7 | 8.656 | .746 |
| 600 | 3.95 | 6.3 | 8.634 | 1.171 |
| 650 | 3.6 | 3.6 | 8.578 | 0 |
| 700 | 3.3 | 3.3 | 8.094 | 0 |
| 750 | 2.85 | 5.2 | 7.683 | 1.207 |
| 800 | 2.4 | 6.7 | 7.132 | .393 |
| 850 | 2.1 | 6.5 | 6.555 | .054 |
| Column Total: | 3.751 |
Similarly the change in emissivity due to a sudden doubling of the atmospheric water vapor concentration can be evaluated provided that Fr remains constant.
CHANGE IN EMISSIVITY DUE TO SUDDEN DOUBLING OF THE ATMOSPHERIC H2O CONCENTRATION:
| Wavenumber (cm^-1) | El=215 K Black Body | Measured Eb | Eh = 270 K Black Body | (Eb - Ec) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 50 | 0.6E | 0.6E | 0.7E | 0 |
| 100 | 1.2E | 1.2E | 1.4E | 0 |
| 150 | 2.0 | 2.0E | 2.8 | 0 |
| 200 | 3.0 | 3.0E | 4.3 | 0 |
| 250 | 3.65 | 4.1 | 5.6 | .346 |
| 300 | 4.3 | 4.9 | 7.1 | .471 |
| 350 | 4.65 | 5.9 | 7.9 | .769 |
| 400 | 4.8 | 6.3 | 8.8 | .938 |
| 450 | 4.8 | 7.3 | 9.25 | 1.096 |
| 500 | 4.55 | 7.8 | 9.5 | 1.045 |
| 550 | 4.3 | 7.7 | 9.5 | 0 - CO2 |
| 600 | 3.95 | 6.3 | 9.3 | 0 - CO2 |
| 650 | 3.6 | 3.6 | 9.0 | 0 - CO2 |
| 700 | 3.3 | 3.3 | 8.5 | 0 - CO2 |
| 750 | 2.85 | 5.2 | 8.0 | 0 - CO2 |
| 800 | 2.4 | 6.7 | 7.4 | .282 |
| 850 | 2.1 | 6.5 | 6.8 | .281 |
| 900 | 1.75 | 6.2 | 6.2 | 0 |
| 950 | 1.5 | 5.6 | 5.6 | 0 |
| 1000 | 1.25 | 4.9 | 4.9 | 0 |
| 1050 | 1.05 | 3.0 | 4.4 | 0 - O3 |
| 1100 | 0.85 | 3.8 | 3.8 | 0 |
| 1150 | 0.7 | 3.3 | 3.3 | 0 |
| 1200 | 0.55 | 3.0 | 3.0 | 0 |
| 1250 | 0.40 | 2.3 | 2.55 | .221 |
| 1300 | 0.3 | 1.0 | 2.15 | .435 |
| 1350 | 0.25 | 1.0 | 1.85 | .398 |
| 1400 | 0.25 | 0.9 | 1.6 | .337 |
| 1450 | 0.2 | 0.7 | 1.35 | .283 |
| 1500 | 0.1 | 0.5 | 1.15 | .248 |
| 1550 | 0.1 | 0.6 | 1.0 | .222 |
| 1600 | 0.05 | 0.7 | 0.8 | .087 |
| 1650 | 0.05 | 0.7 | 0.7 | 0 |
| 1700 | 0.6E | 0.6 | ||
| Column Total: | 7.459 |
CHANGE IN TEMPERATURE:
Recall that:
Ta = Te[(1 - Fr) / Ft]^.25
Assume that Fr = constant. Then:
dTa = Te (.25)[(1 - Fr)/ Ft]^-.75 (1 - Fr)(-Ft^-2)dFt
= (1 / 4) Ta (-dFt / Ft)
INCREASE IN TEMPERATURE DUE TO SUDDEN DOUBLING OF THE ATMOSPHERIC CO2 CONCENTRATION:
(-dFt / Ft) = 3.751 / 123.1 = .03047
Ta = 270 K
giving:
dTa = (270 / 4)(.03071) = 2.058 degrees C
INCREASE IN TEMPERATURE DUE TO SUBSEQUENT DOUBLING OF THE ATMOSPHERIC H2O CONCENTRATION WHILE Fr = CONSTANT:
(-dFt / Ft) = 7.459 / (123.1 - 3.751) = 7.459 / 119.249 = .0625
Ta = 270 + 2.058 = 272.058
giving:
dTa = (272.258 / 4)(.0625) = 4.254 degrees C
ITTERATIVE PROCESS:
Sudden doubling the atmospheric CO2 concentration from its November 1996 value of 360.76 ppmv to a future new value of 2(360.76 ppmv) = 721.52 ppmv causes a step increase in the atmospheric temperature of 2.058 C. This atmospheric temperature increase warms the surface layer of open water, which increases the water vapor pressure and hence the atmospheric water vapor concentration. Assume that the initial open water surface temperature is 15 degrees C = 59.0 degrees F.
1st Itteration:
From a steam table, a 2.058 degree C = 3.7044 degrees F open water surface temperature increase causes a H2O vapor pressure increase of:
(3.7044/3) X (.27494 psia - .24713 psia) = .0343397 psia
At 59 F the absolute pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
.0343397 / .24713 = .13895
The corresponding increase in atmospheric temperature caused by this increased H2O vapor pressure is:
.13895 X 4.254 degrees C = .5911 degrees C
Hence the new value of the atmospheric temperature increase is:
2.058 C + .5911 C = 2.6491 C
2nd Itteration:
From a steam table, a 2.6491 C = 4.768 F open water surface temperature increase causes a H2O vapor pressure increase of:
(4.768 / 4) X (.28480 psia - .24713 psia) = .04490 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.04490 / .24713) = .18169
The corresponding increase in atmospheric temperature caused by this increased H2O vapor pressure is:
.18169 X 4.254 = .7729 C
Hence the new value of the atmospheric temperature increase is:
2.058 + .7729 = 2.8309 C
3rd Itteration:
From a steam table a 2.8309 C = 5.0957 F open water surface temperature increase causes a H2O vapor pressure increase of:
(5.0957 / 5) X (.29497 psia - .24713 psia) = .04876 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.04876 / .24713) = .19728
The corresponding increase in atmospheric temperature caused by this increase in H2O vapor pressure was>
.19728 X 4.254 = .8392 C
Hence the new value of the atmospheric temperature increase is:
2.058 C + .8392 C = 2.8972 C
4th Itteration:
From a steam table a 2.8972 C = 5.215 F open water surface temperature increase causes a H2O vapor pressure increase of:
(5.215 / 5) X (.29497 psia - .24713 psia) = .04990 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.04990 / .24713) = .2019
The corresponding increase in atmospheric temperature caused by this increase in H2O vapor pressure was>
.2019 X 4.254 = .8589 C
Hence the new value of the atmospheric temperature increase is:
2.058 C + .8589 C = 2.917 C
5th Itteration:
From a steam table a 2.917 C = 5.2504 F open water surface temperature increase causes a H2O vapor pressure increase of:
(5.2504 / 5) X (.29497 psia - .24713 psia) = .0502358 psia
At 59 F the absolute H2O vapor pressure was .24713 psia, so the fractional increase in H2O vapor pressure was:
(.0502358 / .24713) = .2033
The corresponding increase in atmospheric temperature caused by this increase in H2O vapor pressure was>
.2033 X 4.254 = .8647 C
Hence the new value of the average atmospheric temperature increase is:
2.058 C + .865 C = 2.923 C
SUMMARY:
Doubling the atmospheric CO2 concentration from its November 1996 value of 360.76 ppmv to a future value of 721.52 ppmv causes a direct atmospheric temperature increase of 2.058 C and if the planetary albedo Fr = constant causes a further average temperature increase of 0.865 C due to an increased atmospheric water vapor concentration for a total atmospheric temperature increase over dry land due to global warming of 2.923 C.
The reader is reminded that 2.923 C is the temperature increase that will occur at the dense cloud level over an uninhabited island in the central Pacific Ocean when the atmospheric CO2 concentration as measured at Mauna Loa, Hawaii is doubled.
The corresponding temperature increase in urban areas is substantially larger due to the proximity of local sources of heat, CO2, and H2O vapor (electric power dissipation, nuclear reactors, cooling towers, combustion of coal, combustion of hydrocarbon fuels) and due to the extensive use of black asphalt (which affects local albedo) for both road surfaces and building roofs. This extra temperature increase is sometimes known as the urban heating effect.
The corresponding temperature increase in polar areas is also substantially larger due to a change in local albedo caused by melting of ice and snow.
Hence, total warming is a combination of global warming and local warming.
IN NOVEMBER 1996:
Tb = 270 K
Ft = Ftb = .7566 from the Emissivity section:
(CO2) = 360.76 ppmv from Carbon dioxide concentration measurements at Mauna Loa for November 1996
CALCULATION OF FUTURE Ft VALUE:
Let Ftc be the value of Ft at an atmospheric CO2 concentration of 721.52 ppmv, twice the November 1996 value. Let:
Tc = Tb + 2.923 C
= 270 C + 2.923 C
= 272.923 C
The warming equation with Fr assumed constant gives:
Tc / Tb = [(Ftb / Ftc)^.25]
or
(Ftb / Ftc) = (Tc / Tb)^4
or
Ftc = Ftb (Tb / Tc)^4
Hence:
(Ftb - Ftc) / Ftb = [1 - (Tb / Tc)^4]
= [1 - .95784]
= .0424
This value is of importance in quantifying the additional rural area irrigation requirements required to maintain the same crop temperature versus time profile before and after the atmospheric CO2 concentration increase.
This web page last updated July 22, 2009.
| Home | Lighting Control | Micro Fusion | Electricity | Climate Change | Contacts | Links |
|---|